Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T01:54:13.982Z Has data issue: false hasContentIssue false
  • English
  • Français

On Divisors of Sums of Integers IV

Published online by Cambridge University Press:  20 November 2018

A. Sárközy  and
C. L. Stewart
A. Sárközy
Affiliation:
Hungarian Academy of Science, Budapest, Hungary
C. L. Stewart
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this article c0, c1, c2, … will denote effectively computable positive absolute constants. Denote the cardinality of a set X by |X|. Let N be a positive integer and let A and B be non-empty subsets of {1, …,N}. Put

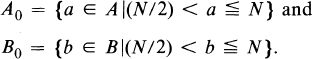
In [3], Balog and Sá;rközy proved that if N > c0 and

(1)

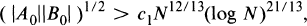
then there exist a0 and b0 with a0 ∊ A0 and b0 ∊ B0 and a prime number p such that

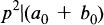
and

(2)

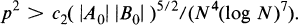
If follows from this result that if |A| ≫ N and |B| ≫ N then there exist a in A and b in B and a prime p such that p2|(a + b) with

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 4 , 01 August 1988 , pp. 788 - 816
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Balog, A. and Sárközy, A., On sums of sequences of integers, I, Acta Arith. 44 (1984), 73–86.Google Scholar
2. Balog, A. and Sárközy, A., On sums of sequences of integers, If Acta Math. Hung. 44 (1984), 169–179.Google Scholar
3. Balog, A. and Sárközy, A., On sums of sequences of integers, III, Acta Math. Hung. 44 (1984), 339–349.Google Scholar
4. Harman, G., Trigonometric sums over primes, I, Mathematika 29 (1981), 249–254.Google Scholar
5. Iwaniec, H. and Pintz, J., Primes in short intervals, Monatshefte Math. 98 (1984), 115–143.Google Scholar
6. Montgomery, H. L. and Vaughan, R. C., The large sieve, Mathematika 20 (1973), 119–134.Google Scholar
7. Pólya, G., Über die Verteilung der quadratischen Reste und Nichtreste, Göttinger Nachrichten (1918), 21–29.Google Scholar
8. Prachar, K., Primzahlverteilung (Springer-Verlag, 1957).Google Scholar
9. Sárközy, A. and Stewart, C. L., On divisors of sums of integers, II, J. reine angew Math. 365 (1986), 171–191.Google Scholar
10. Sárközy, A. and Stewart, C. L., On exponential sums over prime numbers, J. Austral. Math. Soc. Series A, to appear.CrossRefGoogle Scholar
11. Vinogradov, I. M., An asymptotic equality in the theory of quadratic forms, Zh. fiz.-matem. Obshch. Permsk universitet 1 (1918), 18–28.Google Scholar