Published online by Cambridge University Press: 26 February 2021
This paper studies a new Whitney type inequality on a compact domain
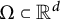 $\Omega \subset {\mathbb R}^d$
that takes the form
$\Omega \subset {\mathbb R}^d$
that takes the form
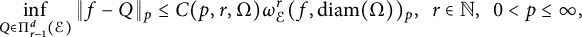
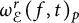 $\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
$\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
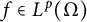 $f\in L^p(\Omega )$
along a finite set of directions
$f\in L^p(\Omega )$
along a finite set of directions
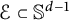 $\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
$\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
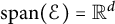 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
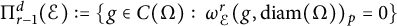 $\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
$\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
 $\mathcal {E}$
for which this inequality holds on every convex body
$\mathcal {E}$
for which this inequality holds on every convex body
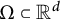 $\Omega \subset {\mathbb R}^d$
, but for every connected
$\Omega \subset {\mathbb R}^d$
, but for every connected
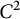 $C^2$
-domain
$C^2$
-domain
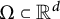 $\Omega \subset {\mathbb R}^d$
, one can choose
$\Omega \subset {\mathbb R}^d$
, one can choose
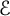 $\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
$\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
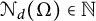 $\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
$\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
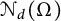 $\mathcal {N}_d(\Omega )$
directions
$\mathcal {N}_d(\Omega )$
directions
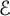 $\mathcal {E}$
such that
$\mathcal {E}$
such that
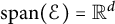 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
 $\Omega $
for all
$\Omega $
for all
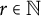 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
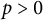 $p>0$
. It is proved that
$p>0$
. It is proved that
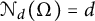 $\mathcal {N}_d(\Omega )=d$
for every connected
$\mathcal {N}_d(\Omega )=d$
for every connected
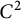 $C^2$
-domain
$C^2$
-domain
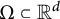 $\Omega \subset {\mathbb R}^d$
, for
$\Omega \subset {\mathbb R}^d$
, for
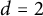 $d=2$
and every planar convex body
$d=2$
and every planar convex body
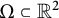 $\Omega \subset {\mathbb R}^2$
, and for
$\Omega \subset {\mathbb R}^2$
, and for
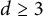 $d\ge 3$
and every almost smooth convex body
$d\ge 3$
and every almost smooth convex body
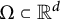 $\Omega \subset {\mathbb R}^d$
. For
$\Omega \subset {\mathbb R}^d$
. For
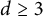 $d\ge 3$
and a more general convex body
$d\ge 3$
and a more general convex body
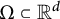 $\Omega \subset {\mathbb R}^d$
, we connect
$\Omega \subset {\mathbb R}^d$
, we connect
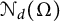 $\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
$\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
 $\Omega $
, proving that if
$\Omega $
, proving that if
 $\Omega $
is X-rayed by a finite set of directions
$\Omega $
is X-rayed by a finite set of directions
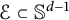 $\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
$\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
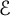 $\mathcal {E}$
admits the directional Whitney inequality on
$\mathcal {E}$
admits the directional Whitney inequality on
 $\Omega $
for all
$\Omega $
for all
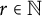 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
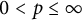 $0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
$0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
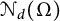 $\mathcal {N}_d(\Omega )$
for
$\mathcal {N}_d(\Omega )$
for
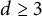 $d\ge 3$
.
$d\ge 3$
.
A slight modification of the proof of the usual Whitney inequality in literature also yields a directional Whitney inequality on each convex body
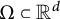 $\Omega \subset {\mathbb R}^d$
, but with the set
$\Omega \subset {\mathbb R}^d$
, but with the set
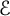 $\mathcal {E}$
containing more than
$\mathcal {E}$
containing more than
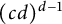 $(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
$(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
The first author was supported by NSERC of Canada Discovery grant RGPIN-2020-03909, and the second author was supported by NSERC of Canada Discovery grant RGPIN-2020-05357.