Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T04:11:36.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On Convergence of Vector valued Pramarts and Subpramarts

Published online by Cambridge University Press:  20 November 2018

Nikos E. Frangos
Nikos E. Frangos*
Affiliation:
The Ohio State University, Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [15] Millet and Sucheston introduced the notion of pramart and subpramart indexed by directed sets, generalizing that of martingale and submartingale, and studied their properties. In particular convergence theorems were proved. In this note we obtain convergence theorems for analogous Banach-valued processes.

Let E be a Banach lattice with the Radon-Nikodym property. Let (Xt, 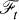, t ∊ J) be an E+-valued subpramart of class (d). Precise definitions are given below (Section 1).

In [10] for J = N, Egghe proved a subpramart convergence theorem under the additional assumption that there is a subsequence {nk} ⊆ N such that 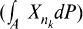converges weakly for each .

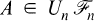Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 2 , 01 April 1985 , pp. 260 - 270
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Astbury, K., A marts indexed by directed sets, Ann. of Prob. 6 (1978), 267–278.Google Scholar
2. Bellow, A., Uniform amarts: A class of asymptotic martingales for which strong almost sure convergence obtains, Z. Wahrscheinlichkeitstheorie Verv. Gebiete 41 (1978), 177–199.Google Scholar
3. Bessaga, C. and Pelczynski, A., Selected topics in infinite dimensional topology, PWN Warsaw, (1975).Google Scholar
4. Chacon, R. and Sucheston, L., On convergence of vector valued asymptotic martingales, Z. Wahrscheinlichkeitstheorie Verv. Gebiete 33 (1975), 55–59.Google Scholar
5. Davis, W. J., Ghoussoub, N. and Lindenstrauss, J., A lattice renorming theorem and applications to vector valued processes. Trans. Am. Math. Soc. 263 (1981), 531–540.Google Scholar
6. Diestel, J. and Uhl, J. Jr., Vector measures, AMS Mathematical Surveys, 15 (Providence, Rhode Island, U.S.A., 1977).CrossRefGoogle Scholar
7. Edgar, G. A., Uniform semiamarts, Ann. Inst. Henri Poincare 75 (1979), 197–203.Google Scholar
8. Edgar, G. A. and Sucheston, L., Amarts: A class of asymptotic martingales, J. Multivariate Anal. 6 (1976), 193–221.Google Scholar
9. Egghe, L., Strong convergence of pramarts in Banach spaces, Can. J. Math. 33 (1981), 357–361.Google Scholar
10. Egghe, L., Strong convergence at positive subpramarts in Banach lattices (to appear in Bull, of the Polish Académie of Sciences).Google Scholar
11. Ghoussoub, N. and Talagrand, M., Order dentability and the Radon-Nikodym property in Banach lattices, Math. Annalen 243 (1979), 217–225.Google Scholar
12. Heinich, H., Convergence de sus-martingales positives dans un Banach reticule, C.R. Acad. Sci. Paris 286 (1978), 279–280.Google Scholar
13. Krickeberg, K., Convergence of martingales with a directed index set, Trans. Am. Math. Soc. 83 (1956), 313–337.Google Scholar
14. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II (Springer-Verlag, Berlin-Heidelberg-New York, 1979).CrossRefGoogle Scholar
15. Millet, A. and Sucheston, L., Convergence of classes of amarts indexed by directed sets, Can. J. Math. 32 (1980), 86–125.Google Scholar
16. Millet, A. and Sucheston, L., A characterization of Vitali conditions in terms of maximal inequalities, Ann. of Prob. 5 (1980), 339–349.Google Scholar
17. Millet, A. and Sucheston, L., On regularity of multiparameter amarts and martingales, Z. Wahrscheinlichkeitstheorie Verv. Gebiete 56, (1981), 21–45.Google Scholar
18. Neveu, J., Discrete-parameter martingales (North-Holland Math Library 10, 1975).Google Scholar
19. Slaby, M., Convergence of positive subpramarts and pramarts in Banach spaces with unconditional bases (to appear in Bull. Acad. Polon. Sci. Ser. Math. Astrom. Phys.).Google Scholar
20. Millet, A. and Sucheston, L., Strong convergence of vector valued pramarts and subpramarts (preprint).Google Scholar
21. Talagrand, M., La structure des espaces de Banach reticules ayant la propriété de Radon-Nikodym, Israel J. of Mathematics 44 (1983), 213–220.Google Scholar