Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T03:04:02.596Z Has data issue: false hasContentIssue false
  • English
  • Français

On Complex Homogeneous Spaces with Top Homology in Codimension Two

Published online by Cambridge University Press:  20 November 2018

D. N. Akhiezer  and
B. Gilligan
D. N. Akhiezer
Affiliation:
B. Spasskaya ul. 33, kv. 33 129010 Moscow Russia, e-mail: [email protected]
B. Gilligan
Affiliation:
Department of Mathematics and Statistics University of Regina Regina, Saskatchewan S4S 0A2, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Define dx to be the codimension of the top nonvanishing homology group of the manifold X with coefficients in 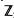2. We investigate homogeneous spaces X := G/H, where G is a connected complex Lie group and H is a closed complex subgroup for which dx = 1,2 and O(X) ≠ ℂ. There exists a fibration π: G/H → G/U such that G/U is holomorphically separable and π*(O(G/U)) = O(G/H), see [11]. We prove the following. If dx = 1, then F := U/H is compact and connected and Y :=G/U is an affine cone with its vertex removed. If dx = 2, then either F is connected with dF = 1 and Y is an affine cone with its vertex removed, or F is compact and connected and dy = 2, where Y is ℂ, the affine quadric Q2, ℙ2 — Q (with Q a quadric curve) or a homogeneous holomorphic 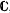* -bundle over an affine cone minus its vertex which is itself an algebraic principal bundle or which admits a two-to-one covering that is.

Keywords

32M10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 5 , 01 October 1994 , pp. 897 - 919
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Abels, H., Some topological aspects of proper group actions; non-compact dimension of groups, J. London Math. Soc. (2), 25(1982), 525–538.Google Scholar
2. Akhiezer, D. N., Dense orbits with two ends, Izv. Acad. Nauk SSSR Ser. Mat. 41(1977), 308–324.Google Scholar
3. Akhiezer, D. N., Complex n-dimensional homogeneous spaces homotopy equivalent to (2n — 2)-dimensional compact manifolds, SelectaMath. Soviet. 3(1983/84), 285–290.Google Scholar
4. Auslander, L. and Tolimieri, R., Splitting theorems and the structure of solvmanifolds, Ann. of Math. (2) 92(1970), 164–173.Google Scholar
5. Barth, W. and Otte, M., Invariante holomorphe Funktionen auf reduktiven Liegruppen, Math. Ann. 201(1973), 97–112.Google Scholar
6. Bialynicki-Birula, A., Hochschild, G. and Mostow, G. D., Extensions of representations of algebraic linear groups. Amer. J. Math. (1) 85(1963), 131–142.Google Scholar
7. Borel, A., Travaux de Mostow sur les espaces homogènes, Séminaires Bourbaki, Exp. 142(1956/57).Google Scholar
8. Che valley, C., Théorie des groupes de Lie II: Groupes algébriques, Hermann, Paris, 1951.Google Scholar
9. Gilligan, B., Ends of homogeneous complex manifolds having nonconstant holomorphic functions, Arch. Math. 37(1981), 544–555.Google Scholar
10. Gilligan, B., On a topological invariant of complex Lie groups and solv-manifolds, C. R. Acad. Sci. Canada 14(1992), 109–114.Google Scholar
11. Gilligan, B. and Huckleberry, A., On non-compact complex nil-manifolds, Math. Ann. 238(1978), 39–49.Google Scholar
12. Huckleberry, A. T., Actions of groups of holomorphic transformations. Several complex variables, VI, 143–196, Encyclopaedia Math. Sci. 69, Springer, Berlin, 1990.Google Scholar
13. Huckleberry, A. T. and Livorni, L., A Classification of Homogeneous Surfaces, Canad. J. Math. (5) 33(1981), 1097–1110.Google Scholar
14. Huckleberry, A. T. and Oeljeklaus, E., Classification Theorems for Almost Homogeneous Spaces, Publ. Inst. E. Cartan 9, Nancy, 1984.Google Scholar
15. Karpelevich, F. I., On afibration of homogeneous spaces, Uspekhi Mat. Nauk 3(69) 11(1956), 131–138; in Russian.Google Scholar
16. Milnor, J., Morse Theory, Princeton University Press, Princeton, 1963.Google Scholar
17. Mostow, G. D., On covariantfibe rings of Klein spaces, I, II, Amer. J. Math. 77(1955), 247–278; 84(1962), 466–474.Google Scholar
18. Mostow, G. D., Some applications of representative functions to solv-manifolds, Amer. J. Math. 93(1971), 11–32.Google Scholar
19. Munkres, J. R., A theorem on open manifolds, preprint.Google Scholar
20. Raghunathan, M. S., Discrete subgroups of Lie groups, Springer-Verlag, New York, 1972.Google Scholar
21. Sukhanov, A. A., Description of observable subgroups of linear algebraic groups, Mat. Sb. (1) 137(1988), 90–102; in Russian.Google Scholar
22. Tits, J., Free subgroups in linear groups, J. Algebra (2) 20(1972), 250–270.Google Scholar