Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T09:57:08.937Z Has data issue: false hasContentIssue false
  • English
  • Français

On Basis-Conjugating Automorphisms of Free Groups

Published online by Cambridge University Press:  20 November 2018

J. McCool
J. McCool*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X = {x1, … xn} be a free generating set of the free group Fn and let H be the subgroup of Aut Fn consisting of those automorphisms α such that α(xi) is conjugate to xi for each i = 1, 2 , …, n. We call H the Z-conjugating subgroup of Aut Fn. In [1] Humphries found a generating set for the isomorphic copy H1 of H consisting of Nielsen transformations

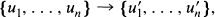
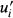where each is conjugate to ui (see remark 1 below). The purpose of this paper is to find a presentation of H (and hence of H1).

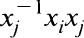Let i ≠ j be elements of {1, 2, …, n}. We denote by (xi; xj) the automorphism of Fn which sends xi to and fixes xk if k ≠ i. Let S be the set of all such automorphisms.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 6 , 01 December 1986 , pp. 1525 - 1529
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Humphries, S. P., On weakly distinguished bases and free generating sets of free groups, Quart. J. Math. Oxford (2) 36 (1985), 215–219.Google Scholar
2. Lyndon, R. and Schupp, P. E., Combinatorial group theory (Springer, 1977).Google Scholar
3. Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Wiley, 1966).Google Scholar
4. McCool, J., A presentation for the automorphism group of a free group of finite rank, J. Lond. Math. Soc. (2) 8 (1974), 259–266.Google Scholar
5. McCool, J., Some finitely presented subgroups of the automorphism group of a free group, J. of Alg. 35 (1975), 205–213.Google Scholar