Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brillhart, John
1980.
Note on irreducibility testing.
Mathematics of Computation,
Vol. 35,
Issue. 152,
p.
1379.
Adleman, Leonard M.
and
Odlyzko, Andrew M.
1983.
Irreducibility testing and factorization of polynomials.
Mathematics of Computation,
Vol. 41,
Issue. 164,
p.
699.
Blecksmith, Richard
and
Nicol, Charles
1993.
Monotonic Numbers.
Mathematics Magazine,
Vol. 66,
Issue. 4,
p.
257.
Gordon, Daniel M.
1993.
Discrete Logarithms in $GF ( P )$ Using the Number Field Sieve.
SIAM Journal on Discrete Mathematics,
Vol. 6,
Issue. 1,
p.
124.
Buhler, J. P.
Lenstra, H. W.
and
Pomerance, Carl
1993.
The development of the number field sieve.
Vol. 1554,
Issue. ,
p.
50.
Konyagin, Sergei
and
Pomerance, Carl
1997.
The Mathematics of Paul Erdös I.
Vol. 13,
Issue. ,
p.
176.
Murty, M. Ram
2002.
Prime Numbers and Irreducible Polynomials.
The American Mathematical Monthly,
Vol. 109,
Issue. 5,
p.
452.
de Sousa Oliveira Santos, José Carlos
2006.
90.38 Another approach to the trisection problem.
The Mathematical Gazette,
Vol. 90,
Issue. 518,
p.
280.
Tzermias, Pavlos
2007.
On Cauchy–Liouville–Mirimanoff Polynomials.
Canadian Mathematical Bulletin,
Vol. 50,
Issue. 2,
p.
313.
Bonciocat, Nicolae Ciprian
and
Zaharescu, Alexandru
2008.
Irreducible multivariate polynomials obtained from polynomials in fewer variables.
Journal of Pure and Applied Algebra,
Vol. 212,
Issue. 10,
p.
2338.
Bonciocat, Anca Iuliana
and
Bonciocat, Nicolae Ciprian
2009.
The Irreducibility of Polynomials That Have One Large Coefficient and Take a Prime Value.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 4,
p.
511.
Filaseta, Michael
and
Gross, Samuel
2014.
49598666989151226098104244512918.
Journal of Number Theory,
Vol. 137,
Issue. ,
p.
16.
焦, 荣政
2017.
Prime Ideals and Krull Dimension of Z[x].
Advances in Applied Mathematics,
Vol. 06,
Issue. 08,
p.
942.
Akman, Fusun
2018.
Polynomials in Base $x$ and the Prime-Irreducible Affinty.
Missouri Journal of Mathematical Sciences,
Vol. 30,
Issue. 2,
Singh, Gajendra
2020.
An Irreducibility Test for Polynomials whose Coefficients are Algebraic Integers.
Indian Journal of Pure and Applied Mathematics,
Vol. 51,
Issue. 1,
p.
171.
Liu, Liwei
Xu, Maozhi
and
Zhou, Guoqing
2021.
Analysis and Improvements to the Special Number Field Sieve for Discrete Logarithm Problems.
p.
45.
Yu, Qian
Liu, Fenjin
Zhang, Hao
and
Heng, Ziling
2021.
Note on graphs with irreducible characteristic polynomials.
Linear Algebra and its Applications,
Vol. 629,
Issue. ,
p.
72.
Phetnun, Phitthayathon
Kanasri, Narakorn Rompurk
Singthongla, Patiwat
and
Solovjovs, Sergejs
2021.
On the Irreducibility of Polynomials Associated with the Complete Residue Systems in any Imaginary Quadratic Fields.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2021,
Issue. ,
p.
1.
Phetnun, Phitthayathon
and
Kanasri, Narakorn R.
2022.
Further irreducibility criteria for polynomials associated with the complete residue systems in any imaginary quadratic field.
AIMS Mathematics,
Vol. 7,
Issue. 10,
p.
18925.
Bonciocat, Ciprian Mircea
and
Bonciocat, Nicolae Ciprian
2022.
Zero-free angular sectors and lens-shaped regions for polynomials, with applications to irreducibility.
Communications in Algebra,
Vol. 50,
Issue. 6,
p.
2604.

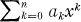 irreducible inZ[x].
irreducible inZ[x]. for 1 ≦ i ≦ n, then f(x) is irreducible inZ[x].
for 1 ≦ i ≦ n, then f(x) is irreducible inZ[x].