Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sossinsky, A. B.
1986.
Tolerance space theory and some applications.
Acta Applicandae Mathematicae,
Vol. 5,
Issue. 2,
p.
137.
Idzik, Adam
1988.
Almost fixed point theorems.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 3,
p.
779.
Barroso, C. S.
Kalenda, O. F. K.
and
Lin, P.-K.
2012.
On the approximate fixed point property in abstract spaces.
Mathematische Zeitschrift,
Vol. 271,
Issue. 3-4,
p.
1271.
Barroso, C.S.
Kalenda, O.F.K.
and
Rebouças, M.P.
2013.
Optimal approximate fixed point results in locally convex spaces.
Journal of Mathematical Analysis and Applications,
Vol. 401,
Issue. 1,
p.
1.
BARROSO, CLEON S.
MBOMBO, BRICE R.
and
PESTOV, VLADIMIR G.
2017.
On topological groups with an approximate fixed point property.
Anais da Academia Brasileira de Ciências,
Vol. 89,
Issue. 1,
p.
19.
Ben Amar, Afif
and
O’Regan, Donal
2022.
Topology and Approximate Fixed Points.
Vol. 71,
Issue. ,
p.
187.


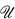 a finite covering of
a finite covering of 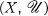 has the
has the 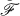 of continuous maps
of continuous maps  there is an
there is an 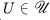 such that
such that 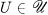 such that
such that  .
.