No CrossRef data available.
Article contents
On a Theorem of Hayman Concerning Quasi-Bounded Functions
Published online by Cambridge University Press: 20 November 2018
Extract
If f(z) is regular in |z| < 1, the expression
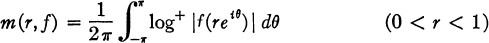
is called the characteristic of f(z). This is the notation of Nevanlinna (4) for the special case of regular functions; in this note it will not be necessary to discuss meromorphic functions. If m(r,f) is bounded for 0 < r < 1, then f(z) is called quasi-bounded in |z| < 1. In particular, every bounded function is quasibounded. The class Q of quasi-bounded functions is important because, for instance, a “Fatou theorem” holds for such functions (4, p. 134).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1959


