Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fjellstedt, Lars
1956.
Einige Sätze über lineare Kongruenzen.
Arkiv för Matematik,
Vol. 3,
Issue. 3,
p.
271.
Stevens, Harlan
1964.
Linear Homogeneous Equations Over Finite Rings.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
532.
Stevens, Harlan
and
Kuty, Larry
1968.
Applications of an elementary theorem to number theory.
Archiv der Mathematik,
Vol. 19,
Issue. 1,
p.
37.
1969.
Geometry of Numbers.
p.
471.
Vegh, Emanuel
1974.
Concerning an Equivalence Relation for Matrices.
The Fibonacci Quarterly,
Vol. 12,
Issue. 4,
p.
391.
Hudson, Richard H.
1974.
On the least K-th power non-residue.
Arkiv för Matematik,
Vol. 12,
Issue. 1-2,
p.
217.
Kaltofen, Erich
and
Rolletschek, Heinrich
1985.
EUROCAL '85.
Vol. 204,
Issue. ,
p.
279.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
1988.
Elementary Theory of Numbers.
Vol. 31,
Issue. ,
p.
482.
Kaltofen, Erich
and
Rolletschek, Heinrich
1989.
Computing greatest common divisors and factorizations in quadratic number fields.
Mathematics of Computation,
Vol. 53,
Issue. 188,
p.
697.
Burger, Edward B.
1996.
Small Solutions to Systems of Linear Congruences over Number Fields.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 3,
Bach, E.
1998.
Efficient prediction of Marsaglia-Zaman random number generators.
IEEE Transactions on Information Theory,
Vol. 44,
Issue. 3,
p.
1253.
BRAUER, ALFRED
2013.
Studies in Mathematics and Mechanics.
p.
20.
Solymosi, Jozsef
2021.
On the Thue–Vinogradov Lemma.
Proceedings of the Steklov Institute of Mathematics,
Vol. 314,
Issue. 1,
p.
325.
Solymosi, Jozsef
2021.
О лемме Туэ-Виноградова.
Труды Математического института имени В. А. Стеклова,
Vol. 314,
Issue. ,
p.
338.
Pollack, Paul
2024.
Z[−5]: Halfway to Unique Factorization.
The American Mathematical Monthly,
Vol. 131,
Issue. 8,
p.
712.


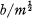 is not an integer, then it is always possible to find integers x and y not both zero such that
is not an integer, then it is always possible to find integers x and y not both zero such that