Published online by Cambridge University Press: 22 November 2019
Let 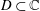 $D\subset \mathbb{C}$ be a domain with
$D\subset \mathbb{C}$ be a domain with 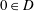 $0\in D$. For
$0\in D$. For 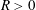 $R>0$, let
$R>0$, let 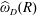 $\widehat{\unicode[STIX]{x1D714}}_{D}(R)$ denote the harmonic measure of
$\widehat{\unicode[STIX]{x1D714}}_{D}(R)$ denote the harmonic measure of 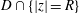 $D\cap \{|z|=R\}$ at
$D\cap \{|z|=R\}$ at 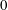 $0$ with respect to the domain
$0$ with respect to the domain 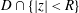 $D\cap \{|z|<R\}$ and let
$D\cap \{|z|<R\}$ and let 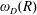 $\unicode[STIX]{x1D714}_{D}(R)$ denote the harmonic measure of
$\unicode[STIX]{x1D714}_{D}(R)$ denote the harmonic measure of 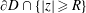 $\unicode[STIX]{x2202}D\cap \{|z|\geqslant R\}$ at
$\unicode[STIX]{x2202}D\cap \{|z|\geqslant R\}$ at 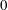 $0$ with respect to
$0$ with respect to 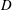 $D$. The behavior of the functions
$D$. The behavior of the functions 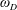 $\unicode[STIX]{x1D714}_{D}$ and
$\unicode[STIX]{x1D714}_{D}$ and 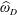 $\widehat{\unicode[STIX]{x1D714}}_{D}$ near
$\widehat{\unicode[STIX]{x1D714}}_{D}$ near 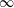 $\infty$ determines (in some sense) how large
$\infty$ determines (in some sense) how large 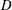 $D$ is. However, it is not known whether the functions
$D$ is. However, it is not known whether the functions 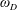 $\unicode[STIX]{x1D714}_{D}$ and
$\unicode[STIX]{x1D714}_{D}$ and 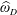 $\widehat{\unicode[STIX]{x1D714}}_{D}$ always have the same behavior when
$\widehat{\unicode[STIX]{x1D714}}_{D}$ always have the same behavior when 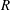 $R$ tends to
$R$ tends to 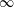 $\infty$. Obviously,
$\infty$. Obviously, 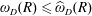 $\unicode[STIX]{x1D714}_{D}(R)\leqslant \widehat{\unicode[STIX]{x1D714}}_{D}(R)$ for every
$\unicode[STIX]{x1D714}_{D}(R)\leqslant \widehat{\unicode[STIX]{x1D714}}_{D}(R)$ for every 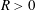 $R>0$. Thus, the arising question, first posed by Betsakos, is the following: Does there exist a positive constant
$R>0$. Thus, the arising question, first posed by Betsakos, is the following: Does there exist a positive constant 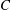 $C$ such that for all simply connected domains
$C$ such that for all simply connected domains 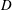 $D$ with
$D$ with 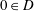 $0\in D$ and all
$0\in D$ and all 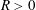 $R>0$,
$R>0$, 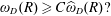 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{D}(R)\geqslant C\widehat{\unicode[STIX]{x1D714}}_{D}(R)?\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{D}(R)\geqslant C\widehat{\unicode[STIX]{x1D714}}_{D}(R)?\end{eqnarray}$$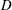 $D$, we prove that the answer is positive. We also find the value of the optimal constant for starlike domains.
$D$, we prove that the answer is positive. We also find the value of the optimal constant for starlike domains.