Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T17:42:09.254Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Linear Refinement of the Prékopa-Leindler Inequality

Published online by Cambridge University Press:  20 November 2018

Andrea Colesanti ,
Eugenia Saorín Gómez  and
Jesús Yepes Nicolás
Andrea Colesanti
Affiliation:
Dipartimento di Matematica “U. Dini”, Viale Morgagni 67/A, 50134-Firenze, Italy e-mail: [email protected]
Eugenia Saorín Gómez
Affiliation:
Institut für Algebra und Geometrie, Otto-von-Guericke Universität Magdeburg, Universitätsplatz 2, D-39106-Magdeburg, Germany e-mail: [email protected]
Jesús Yepes Nicolás
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100-Murcia, Spain e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 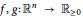$f,\,g:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}_{\ge 0}}$ are non-negative measurable functions, then the Prékopa–Leindler inequality asserts that the integral of the Asplund sum (provided that it is measurable) is greater than or equal to the 0-mean of the integrals of 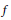$f$ and 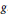$g$. In this paper we prove that under the sole assumption that 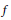$f$ and 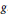$g$ have a common projection onto a hyperplane, the Prékopa–Leindler inequality admits a linear refinement. Moreover, the same inequality can be obtained when assuming that both projections (not necessarily equal as functions) have the same integral. An analogous approach may be also carried out for the so-called Borell-Brascamp-Lieb inequality.

Keywords

52A4026D1526B25Prékopa–Leindler inequalitylinearityAsplund sumprojectionsBorell–Brascamp–Lieb inequality
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 4 , 01 August 2016 , pp. 762 - 783
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bonnesen, T. and Fenchel, W.,Théorie der konvexen Korper. Berichtiger reprint. Springer, Berlin,1974.Google Scholar
[2] Borell, C., Convex set functions in d-space. Period. Math. Hungar. 6(1975), no. 2,111–136. http://dx.doi.Org/10.1007/BF02018814 Google Scholar
[3] Brascamp, H. J. and Lieb, E. H., On extensions of the Brunn-Minkowski and Prékopa-Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation. J. Functional Analysis 22(1976), no. 4, 366–389.http://dx.doi.Org/10.1016/0022-1236(76)90004-5 Google Scholar
[4] Colesanti, A. and Fragalá, I., The first variation of the total mass of log-concave functions and related inequalities. Adv. Math. 244(2013), 708–749. http://dx.doi.Org/10.1016/j.aim.2013.05.015 Google Scholar
[5] Danes, S. and Uhrin, B., On a class of integral inequalities and their measure-theoretic consequences. J. Math. Anal. Appl. 74(1980), no. 2, 388–400. http://dx.doi.Org/10.1016/0022-247X(80)90136-5 Google Scholar
[6] Diskant, V. I., A counterexample to an assertion of Bonnesen and Fenchel. (Russian) Ukrain.Geom. Sb. No. 27(1984), 31–33.Google Scholar
[7] Dubuc, S., Critéres de convexité et inégalités intégrales. Ann. Inst. Fourier (Grenoble) 27(1977),no.1, x, 135–165.Google Scholar
[8] Evans, L. C. and Gariepy, R.,Measure theory and fine properties of functions. Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1992.Google Scholar
[9] Gardner, R. J., The Brunn-Minkowski inequality. Bull. Amer. Math. Soc. 39(2002), no. 3, 355–405.http://dx.doi.org/10.1090/S0273-0979-02-00941-2 Google Scholar
[10] Giannopoulos, A., Convex geometric analysis. Private Notes (Unpublished Manuscript), 2009. http://www.math.uoc.gr/~apostolo/notes.ps Google Scholar
[11] Gruber, P. M., Convex and discrete geometry. Grundlehren der Mathematischen Wissenschaften, 336. Springer, Berlin, 2007.Google Scholar
[12] Henstock, R. and Macbeath, A. M., On the measure of sum-sets. I. The theorems ofBrunn, Minkowski, and Lusternik. Proc. London Math. Soc. 3(1953), no. 3,182–194.http://dx.doi.Org/10.1112/plms/s3-3.1.182 Google Scholar
[13] Hernández Cifre, M. A. and Yepes Nicolás, J., Refinements of the Brunn-Minkowski inequality. J.Convex Anal. 21(2014), no. 3,1–17.Google Scholar
[14] Hardy, G. H., Littlewood, J. E., and Pólya, G., Inequalities. Cambridge Mathematical Library, Reprint of the 1952 edition, Cambridge University Press, Cambridge, 1988.Google Scholar
[15] Kawohl, B., Rearrangements and convexity of level sets in PDE. Lecture Notes in Mathematics, 1150. Springer-Verlag, Berlin, 1985.Google Scholar
[16] Klartag, B. and Milman, V. D., Geometry of log-concave functions and measures. Geom. Dedicata 112(2005), 169–182.http://dx.doi.Org/10.1007/s10711-004-2462-3 Google Scholar
[17] Leindler, L., On certain converse of Hölder's inequality. II. Acta Math. Sci.(Szeged), 33(1972, no. 3-4,) 217–223.Google Scholar
[18] Marsiglietti, A., On improvement of the concavity of convex measures. Proc. Amer. Math. Soc. 144(2016), no. 2, 775–786.http://dx.doi.org/10.1090/proc/12694 Google Scholar
[19] Ohmann, D., Über den Brunn-Minkowskischen Satz. Comment. Math. Helv 29(1955), 215–222.http://dx.doi.org/10.1007/BF02564280 Google Scholar
[20] Pisier, G., The volume of convex bodies and Banach space geometry. Cambridge Tracts in Mathematics, 94. Cambridge University Press, Cambridge,1989.Google Scholar
[21] Prékopa, A., Logarithmic concave measures with application to stochastic programming. Acta Sci. Math. (Szeged), 32(1971), 301–316.Google Scholar
[22] Rockafellar, R. T., Convex analysis. Princeton Mathematical Series 28. Princeton University Press, Princeton, New Jersey, 1970.Google Scholar
[23] Rockafellar, R. T., and Wets, R. J.-B., Variational analysis. Grundlehren der Mathematischen Wissenschaften 317. Springer-Verlag, Berlin, 1998.Google Scholar
[24] Schneider, R., Convex bodies: the Brunn-Minkowski theory. Second edition. Encyclopedia of Mathematics and its Applications, 151. Cambridge University Press, Cambridge, 2014.Google Scholar