Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-06T14:28:54.953Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Discriminant Inequality

Published online by Cambridge University Press:  20 November 2018

L. J. Mordell
L. J. Mordell*
Affiliation:
Mount Allison University, Sackville, New Brunswick, Canada St John s College, Cambridge, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following result has been conjectured by Dr. Birch. Let z1 z2, . . . , zn be any n complex numbers such that

(1)

Then

(2)

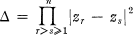
attains its greatest value when the z are at the vertices of a regular n-sided polygon inscribed in the circle |z| =1.

It seems to be difficult to prove this but Dr. Birch informs me that some work by Mullholland shows that the result is false for large n. I can, however, prove that the result is true for n = 3, and then Δ ≤ 27. The suggested general result would be Δ ≤ nn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 699 - 704
Copyright
Copyright © Canadian Mathematical Society 1960

References

1 ”Inequalities between the geometric mean difference and the polar moments of a plane distribution,” Journal of the London Mathematical Society, 33 (1958) 260-269.