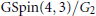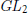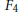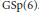Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pollack, Aaron
Wan, Chen
and
Zydor, Michał
2019.
A G2-period of a Fourier coefficient of an Eisenstein series on E6.
Israel Journal of Mathematics,
Vol. 234,
Issue. 1,
p.
229.
Pollack, Aaron
Wan, Chen
and
Zydor, Michał
2021.
On the residue method for period integrals.
Duke Mathematical Journal,
Vol. 170,
Issue. 7,