Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-19T02:11:12.599Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Conjecture of Erdös, Faber, and Lovász about n-Colorings

Published online by Cambridge University Press:  20 November 2018

Neil Hindman
Neil Hindman*
Affiliation:
Howard University, Washington, D.C.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

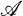Let be a finite family of finite sets with the property that |A ∩ B| ≦ 1 whenever A and B are distinct members of 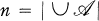. It is a conjecture of Erdös, Faber, and Lovász ([1] a 50 pound problem and [2] a 100 dollar problem) that there is an n-coloring of 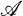(i.e., a function 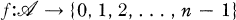such that A ∩ B = ∅ whenever A and B are distinct members of 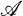with f(A) = f(B). They actually state the conjecture in a different form. They actually state the conjecture in a different form. Namely, if n is a positive integer and 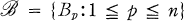is a family of n sets satisfying (1) |Bp| = n for each p and (2) |Bp ∩ Bq| ≦ 1 when p ≠ q, then there is an n-coloring of the elements of 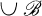so that each set Bp gets all n colors. The equivalence of the two forms is easily seen by interchanging the roles of elements and sets.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 563 - 570
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Erdos, P., Problems and results in graph theory and combinatorial analysis, Proceedings of the Fifth British Combinatorial Conference, 169-92. Congressus Numerantium, No. XV, Utilitas Math. (1976).Google Scholar
2. Erdos, P., Some recent problems and results on graph theory, combinatorics and number theory, Proceedings of the Seventh Southeastern Conference on Combinatorics, Graph Theory and Computing, 3-14. Congressus Numerantium, No. XVII, Utilitas Math. (1976).Google Scholar