Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T10:54:14.205Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Chen and Yui: Resultants and discriminants

Part of: Computational number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 December 2020

Dongxi Ye
Dongxi Ye*
Affiliation:
School of Mathematics (Zhuhai), Sun Yat-sen University, Zhuhai, P.R. China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In [5], Chen and Yui conjectured that Gross–Zagier type formulas may also exist for Thompson series. 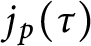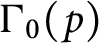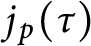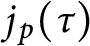In this work, we verify Chen and Yui’s conjecture for the cases for Thompson series $j_{p}(\tau )$ for $\Gamma _{0}(p)$ for p prime, and equivalently establish formulas for the prime decomposition of the resultants of two ring class polynomials associated to $j_{p}(\tau )$ and imaginary quadratic fields and the prime decomposition of the discriminant of a ring class polynomial associated to $j_{p}(\tau )$ and an imaginary quadratic field. Our method for tackling Chen and Yui’s conjecture on resultants can be used to give a different proof to a recent result of Yang and Yin. In addition, as an implication, we verify a conjecture recently raised by Yang, Yin, and Yu.

Keywords

The Chen–Yui conjecturediscriminantprime decompositionresultantring class polynomialssingular values

MSC classification

Primary: 11F03: Modular and automorphic functions
Secondary: 11F11: Holomorphic modular forms of integral weight 11Y05: Factorization
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 486 - 526
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dongxi Ye is supported by the Natural Science Foundation of China (grant No.11901586), the Natural Science Foundation of Guangdong Province (grant No.2019A1515011323), and the Sun Yat-sen University Research Grant for Youth Scholars (grant no.19lgpy244).

References

Borcherds, R. E., Automorphic forms on ${O}_{s+2,2}\left(\mathbb{R}\right)$ and infinite products. Invent. Math. 120(1995), 161–213.CrossRefGoogle Scholar
Borcherds, R. E., Automorphic forms with singularities on Grassmannians. Invent. Math. 132(1998), 491–562.CrossRefGoogle Scholar
Bruinier, J. H., Kudla, S., and Yang, T., Special values of Green functions at big CM points . Int. Math. Res. Not. 9(2012), 1917–1967.Google Scholar
Bruinier, J. H. and Yang, T., Faltings heights of CM cycles and derivatives of $L$ -functions . Invent. Math. 177(2009), 631–681.CrossRefGoogle Scholar
Chen, I. and Yui, N., Singular values of Thompson series . In: Arasu, K. T., Dillon, J. F., Harada, K., Sehgal, S., and Solomon, R. (eds.), Groups, difference sets, and the monster (Columbus, OH, 1993), Ohio State Univ. Math. Res. Inst. Publ., 4, de Gruyter, Berlin, Germany, 1996, pp. 255–326.Google Scholar
Conway, J. and Norton, S., Monstrous moonshine . Bull. Lond. Math. Soc. 11(1979), 308–339.CrossRefGoogle Scholar
Cox, D., Primes of the form x2+ny2 . Wiley, Hoboken, NJ, 1989.Google Scholar
Gross, B., Kohnen, W., and Zagier, D., Heegner points and derivatives of L-series. II . Math. Annalen. 278(1987), 497–562.CrossRefGoogle Scholar
Gross, B. and Zagier, D., On singular moduli . J. Reine Angew. Math. 355(1985), 191–220.Google Scholar
Gross, B. and Zagier, D., Heegner points and derivative of $L$ -series . Invent. Math. 85(1986), 225–320.CrossRefGoogle Scholar
Iwaniec, H., Spectral methods of automorphic forms. Graduate Studies in Mathematics, 53, American Mathematical Society, Providence, RI, 2002.Google Scholar
Kudla, S. S., Integrals of Borcherds forms . Compos. Math. 137(2003), 293–349.CrossRefGoogle Scholar
Kudla, S. S. and Yang, T., Eisenstein series for $\mathrm{SL}(2)$ . Sci. China Math. 53(2010), 2275–2316.CrossRefGoogle Scholar
Schofer, J., Borcherds forms and generalizations of singular moduli . J. Reine Angew. Math. 629(2009), 1–36.CrossRefGoogle Scholar
Shimura, G., Arithmetic of quadratic forms. Springer, New York, NY, 2010.CrossRefGoogle Scholar
Yang, T. and Yin, H., Difference of modular functions and their CM value factorization . Trans. Amer. Math. Soc. 371(2019), 3451–3482.CrossRefGoogle Scholar
Yang, T., Yin, H., and Yu, P., The lambda invariants at CM points . Int. Math. Res. Not. rnz230(2019). https://doi.org/10.1093/imrn/rnz230 Google Scholar
Ye, D., On the generating function of a canonical basis for . Results Math. 74(2019), no. 2.CrossRefGoogle Scholar
Ye, D., Revisiting the Gross–Zagier discriminant formula . Math. Nachr. 293(2020), 1801–1826.CrossRefGoogle Scholar
Ye, D., On a zeta function associated to a quadratic order . Results Math. 75(2020), no. 27.CrossRefGoogle Scholar
Ye, D., Difference of a Hauptmodul for and certain Gross–Zagier type CM value formulas. Preprint, 2020. arxiv:1708.08783 Google Scholar