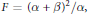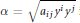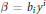Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moghaddam, H R Salimi
2008.
The flag curvature of invariant (α, β)-metrics of type \frac{(\alpha+\beta)^2}{\alpha}.
Journal of Physics A: Mathematical and Theoretical,
Vol. 41,
Issue. 27,
p.
275206.
Shen, Zhongmin
2009.
On Projectively Flat (α, β)-metrics.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 1,
p.
132.
Cui, Ningwei
and
Shen, Yi-Bing
2009.
Projective change between two classes of(α,β)-metrics.
Differential Geometry and its Applications,
Vol. 27,
Issue. 4,
p.
566.
Li, Benling
Shen, Yibing
and
Shen, Zhongmin
2009.
On a class of Douglas metrics.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 46,
Issue. 3,
p.
355.
Zhou, Linfeng
2010.
A local classification of a class of (α,β) metrics with constant flag curvature.
Differential Geometry and its Applications,
Vol. 28,
Issue. 2,
p.
170.
Zohrehvand, Mosayeb
and
Rezaii, Morteza MirMohamad
2012.
On the non-Riemannian quantity H of an (α,β)-metric.
Differential Geometry and its Applications,
Vol. 30,
Issue. 5,
p.
392.
Kampalappa, Narasimhamurthy Senajji
and
Mylarappa, Vasantha Dogehalli
2012.
Projective Change between Two Finsler Spaces with (α, β)- metric.
Kyungpook mathematical journal,
Vol. 52,
Issue. 1,
p.
81.
Chen, Bin
Shen, Zhongmin
and
Zhao, Lili
2013.
On a class of Ricci-flat Finsler metrics in Finsler geometry.
Journal of Geometry and Physics,
Vol. 70,
Issue. ,
p.
30.
YANG, GUOJUN
2013.
ON A CLASS OF SINGULAR PROJECTIVELY FLAT FINSLER METRICS WITH CONSTANT FLAG CURVATURE.
International Journal of Mathematics,
Vol. 24,
Issue. 10,
p.
1350087.
Chen, Guangzu
Cheng, Xinyue
and
Yuan, Mingao
2013.
On a class of projectively flat Finsler metrics with weakly isotropic flag curvature.
Periodica Mathematica Hungarica,
Vol. 67,
Issue. 2,
p.
155.
Binh, T. Q.
Kertész, D. Cs.
and
Tamássy, L.
2013.
On projectively flat Finsler spaces.
Acta Mathematica Hungarica,
Vol. 141,
Issue. 4,
p.
383.
Yang, Guo Jun
2013.
On a class of two-dimensional projectively flat finsler metrics with constant flag curvature.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 5,
p.
959.
Yang, Guojun
Mira, P.
and
Mokhov, O.
2013.
On a Class of Two‐Dimensional Douglas and Projectively Flat Finsler Metrics.
The Scientific World Journal,
Vol. 2013,
Issue. 1,
Alimohammadi, Ahmad
2014.
On the Class of(q,α,β)-Metrics.
ISRN Geometry,
Vol. 2014,
Issue. ,
p.
1.
余, 昌涛
2015.
A Characterization for Locally Projectively Flat Berwald Type (α, β)-Metrics.
Pure Mathematics,
Vol. 05,
Issue. 04,
p.
150.
Yu, Changtao
and
Zhu, Hongmei
2015.
Projectively flat general (α,β)-metrics with constant flag curvature.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
1222.
Yu, Changtao
2016.
Deformations and Hilbert’s fourth problem.
Mathematische Annalen,
Vol. 365,
Issue. 3-4,
p.
1379.
Tayebi, A.
and
Barzegari, M.
2016.
Generalized Berwald spaces with(α,β)-metrics.
Indagationes Mathematicae,
Vol. 27,
Issue. 3,
p.
670.
Cheng, Xinyue
Ma, Xiaoyu
Shen, Yuling
and
Liu, Shuhua
2017.
Lie Groups, Differential Equations, and Geometry.
p.
247.
Guo, Enli
and
Mo, Xiaohuan
2018.
The Geometry of Spherically Symmetric Finsler Manifolds.
p.
67.