Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jamison, Benton
1964.
Asymptotic behavior of successive iterates of continuous functions under a Markov operator.
Journal of Mathematical Analysis and Applications,
Vol. 9,
Issue. 2,
p.
203.
Jamison, Benton
1965.
Ergodic decompositions induced by certain Markov operators.
Transactions of the American Mathematical Society,
Vol. 117,
Issue. 0,
p.
451.
Iosifescu, M.
and
Theodorescu, R.
1965.
On Bush-Mosteller stochastic models for learning.
Journal of Mathematical Psychology,
Vol. 2,
Issue. 1,
p.
196.
Norman, M.Frank
1968.
Some convergence theorems for stochastic learning models with distance diminishing operators.
Journal of Mathematical Psychology,
Vol. 5,
Issue. 1,
p.
61.
Frank Norman, M.
1970.
A uniform ergodic Theorem for certain Markov operators on Lipschitz functions on bounded metric spaces.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 15,
Issue. 1,
p.
51.
1972.
Markov Processes and Learning Models.
Vol. 84,
Issue. ,
p.
263.
Keane, Michael
1972.
Strongly mixingg-measures.
Inventiones Mathematicae,
Vol. 16,
Issue. 4,
p.
309.
Iosifescu, Marius
1986.
The Craft of Probabilistic Modelling.
Vol. 1,
Issue. ,
p.
250.
Viand, M.-C.
1991.
Random Iterations and Kalman Filtering.
Theory of Probability & Its Applications,
Vol. 35,
Issue. 4,
p.
737.
Dinwoodie, I.H.
1994.
Occupation measures for chains of infinite order.
Stochastic Processes and their Applications,
Vol. 50,
Issue. 1,
p.
73.
Dinwoodie, I. H.
1994.
Observing a preferred distribution.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
585.


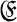 ⊂ β (E) two tribes. For every
⊂ β (E) two tribes. For every 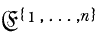 . For every
. For every 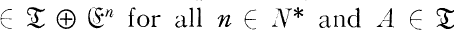 .
.