Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:35:06.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Obstructions to Liftings in Commutative Squares

Published online by Cambridge University Press:  20 November 2018

Irwin S. Pressman
Irwin S. Pressman*
Affiliation:
The Ohio State University, Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A commutative square (1) of morphisms is said to have a lifting if there is a morphism λ: B1 → A2 such that λϕ1 = α and ϕ2λ = β

1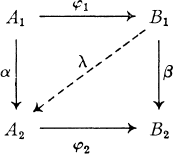

Let us assume that we are working in a fixed abelian category 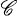. Therefore, ϕi will have a kernel “Ki” and a cokernel “Ci” for i = 1, 2. Let k : K1 → K2 and c: C1 → C2 denote the canonical morphisms induced by α and β.

We shall construct a short exact sequence (s.e.s.)

2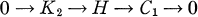

using the data of (1). We shall prove that (1) has a lifting if and only if k = 0, c = 0, and (2) represents the zero class in Ext1(C1, K2). Furthermore, if (1) has one lifting, then the liftings will be in one-to-one correspondence with the elements of the set |Hom(G1, K2)|.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 6 , December 1971 , pp. 977 - 982
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Hilton, Peter J., Homotopy theory and duality (Gordon and Breach, New York, 1965).Google Scholar
2. MacLane, Saunders, Homology (Springer, Berlin, 1963).Google Scholar
3. Olum, Paul, Homology of squares and factoring of diagrams, pp. 480–489, Lecture Notes in Mathematics, No. 99 (Springer-Verlag, New York, 1969).Google Scholar
4. Pressman, Irwin S., Endomorphisms of exact sequences, Bull. Amer. Math. Soc. 77 (1971), 239–242.Google Scholar