Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T15:04:59.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Number of Right Ideals and a q-analogue of Indecomposable Permutations

Published online by Cambridge University Press:  20 November 2018

Roland Bacher  and
Christophe Reutenauer
Roland Bacher
Affiliation:
Univ. Grenoble Alpes, Institut Fourier (CNRS UMR 5582), 100 rue des Maths, F-38000 Grenoble, France e-mail: [email protected]
Christophe Reutenauer
Affiliation:
Département de Mathématiques, UQAM, Case Postale 8888 Succ. Centre-ville, Montréal H3C 3P8, Québec [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the number of right ideals of codimension $n$ in the algebra of noncommutative Laurent polynomials in two variables over the finite field 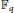${{\mathbb{F}}_{q}}$ is equal to

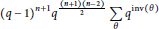$${{\left( q-1 \right)}^{n+1}}_{{}}{{q}^{\frac{\left( n+1 \right)\left( n-2 \right)}{2}}}\sum\limits_{\theta }{{{q}^{inv\left( \theta \right)}}}$$
,

where the sum is over all indecomposable permutations in 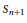${{S}_{n+1}}$ and where inv 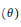$\left( \theta \right)$ stands for the number of inversions of 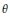$\theta $ .

Keywords

05A1505A19Keywordspermutationindecomposable permutationsubgroups of free groups
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 481 - 503
Copyright
Copyright © Canadian Mathematical Society 2016

References

[AS]Aguiar, M. and Sottile, F., Structure of the Malvenuto-Reutenauer Hopf algebra of permutations. Adv. Math.191(2005), 225–275 http://dx.doi.org/10.1016/j.aim.2004.03.007.Google Scholar
[B]Bona, M., Combinatorics of permutations. Second ed., Discrete Mathematics and its Applications, CRC Press, Boca Raton, FL, 2012.http://dx.doi.org/10.1201/b12210 Google Scholar
[BPR]Berstel, J., Perrin, D., and Reutenauer, C., Codes and automata. Enclyclopedia and its Applications, 129, Cambridge University Press, Cambridge, 2010.Google Scholar
[BR]R. Bacher, and C. Reutenauer, , The number of right ideals of given codimension over a finite field. In: Noncommutative birational geometry, representations and combinatorics, Contemp. Math., 592, American Mathematical Society, Providence, RI, 2013, pp. 1–18.http://dx.doi.org/10.1090/conm/592/11865 Google Scholar
[C]Cohn, P. M., Free ideal rings. J. Algebra 1 (1964),47–69.http://dx.doi.org/10.1016/0021-8693(64)90007-9 Google Scholar
[Cm]Comtet, L.,Sur les coefficients de l'inverse de la série formelle Σn!tn. C. R. Acad. Sci. Paris Sér. A–B 275 (1972),A569–A572.Google Scholar
[Cr]Cori, R., Indecomposable permutations, hypermaps and labeled Dyck paths. J. Combin. Theory Ser. A 116 (2009), no. 8, 1326–1343. http://dx.doi.org/10.1016/j.jcta.2009.02.008.Google Scholar
[DF1]Dress, A.W.M. and Franz, R., Parametrizing the subgroups of ûnite index in a free group and related topics. Bayreuth. Math. Schr. 20(1958), 1–8.Google Scholar
[DFz]Dress, A.W.M. ,Zur Parametrisierung von Untergruppen freier Gruppen. Beiträge Algebra Geom. 24(1987),125–134.Google Scholar
[GR]Garsia, A. M. and Remmel, J. B., q-counting rook conûgurations and a formula of Frobenius. J. Combin.Theory Ser. A 41(1986), no. 2, 246–275.http://dx.doi.org/10.1016/0097-3165(86)90083-X Google Scholar
[Hg]Haglund, J., q-rooks polynomials and matrices over finite fields. Adv. in Appl. Math. 20(1998), no.4,450–487 http://dx.doi.org/10.1006/aama.1998.0582.Google Scholar
[H]Hall, M., Jr., Subgroups of finite index in free groups. Canad. J. Math.1(1949),187–190.http://dx.doi.org/10.4153/CJM-1949-017-2 Google Scholar
[LLMPSZ]Lewis, J. B., Liu, R. I., Morales, A. H. , Panova, G., Sam, S. V., Zhang, Y. X. , Matrices with restricted entries and q-analogues of permutations. J. Comb. 2(2011), no.3,355–395.http://dx.doi.org/10.4310/JOC.2011.v2.n3.a2.Google Scholar
[OEIS] Sloane, N. J. A., The electronic encyclopedia of integer sequences. http://oeis.org.Google Scholar
[OR]de Mendez, P. Ossona and Rosenstiehl, P., Transitivity and connectivity of permutations. Combinatorica 24(2004),no.3,487–501. http://dx.doi.org/10.1007/s00493-004-0029-4 Google Scholar
[P]Pirashvili, T., Sets with two associative operations. Cent. Eur. J. Math. 1(2003), no. 2, 169–183. http://dx.doi.org/10.2478/BF02476006 Google Scholar
[PR]Poirier, S. and Reutenauer, C., Algébre de Hopf de tableaux. Ann. Sci. Math. Québec 19(1995),no.1,79–90.Google Scholar
[R]Reineke, M., Cohomology of noncommutative Hilbert schemes. Algebr. Represent.Theory 8(2005), no.4,541–561. http://dx.doi.org/10.1007/s10468-005-8762-y Google Scholar
[Si]Sillke, T., Zur Kombinatorik von Permutationen, Séminaire Lotharingien de Combinatoire (Oberfranken,1990), Publ. Inst. Rech. Math. Av.,413, Univ. Louis Pasteur, Strasbourg,1990, pp.111–119.Google Scholar