Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:03:52.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Notions De Base Pour L'Arthmetique De Fq((1/t))

Published online by Cambridge University Press:  20 November 2018

Yves Hellegouarch
Yves Hellegouarch*
Affiliation:
Université de Caen, Caen Cedex, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Le but de ce travail est de définir un certain nombre d'objets de Fq((1/t) et de fonctions

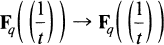
qui sont analogues à des objets classiques de R(ou C) et à des fonctions classiques R → R (ou C → C) : par exemple ζ(l), ζ(2), etc., fractions continues, domaine fondamental du “demi-plan” de Poincaré, séries d'Eisenstein, fonctions multiplement périodiques.

Un tel travail avait été entrepris autrefois par E. Artin [2], mais dans un autre esprit, et la fonction zéta que j'ai définie dans [7] n'est pas celle d'Artin, mais celle de Carlitz [3].

L'intersection de la thèse d'Artin et de ce travail n'est donc pas vide, mais elle n'est pas non plus très étendue bien que je me sois limité aux définitions et aux propriétés les plus élémentaires. En revanche, par son esprit, ce travail se rapproche davantage du point de vue de Carlitz.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 4 , 01 August 1988 , pp. 817 - 832
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Artin, E., Algebraic number and algebraic functions (Gordon and Breach, 1967).Google Scholar
2. Artin, E., Quadratische Körpern im Gebiete der köheren Kongruenzen in The collected papers of Emil Artin (Addison-Wesley, 1965).Google Scholar
3. Carlitz, L., On certain functions connected with polynomials in a Galois field, Duke Math. J. 1 (1935), 137–168.Google Scholar
4. Damamme, G., Irrationalité de ζ(s) dans le corps des séries formelles F q ((1/t)), C.R. Math. Ac. Sci. Canada 9 (1987), 207–212.Google Scholar
5. Geijsel, J. M., Transcendence infields of positive characteristic, Thèse (1978), Amsterdam.Google Scholar
6. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (Oxford, 1954).Google Scholar
7. Hellegouarch, Y., Propriétés arithmétiques des séries formelles à coefficients dans un corps fini, C.R. Math. Acad. Sci. Canada 8 (1986), 115–120.Google Scholar
8. Ouro-Sama, S., Algèbre géométrique d'une extension quadratique avec référence spéciale aux corps de séries formelles, Thèse de 3ème cycle, Université de Caen (1987).Google Scholar
9. Rademacher, H., Topics in analytic number theory (Springer, 1973).CrossRefGoogle Scholar
10. Serre, J. P., Cours d'arithmétique (P.U.F., 1970).Google Scholar
11. Wade, L. I., Certain quantities transcendental over GF(pn, x), II, Duke Math. J. 10 (1943), 587–594.Google Scholar
12. Weil, A., Elliptic functions according to Eisenstein and Kronecker (Springer, 1976).CrossRefGoogle Scholar