Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T02:00:34.755Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the mod 2 Cohomology of BŜOn〈l6〉

Published online by Cambridge University Press:  20 November 2018

Tze-Beng Ng
Tze-Beng Ng*
Affiliation:
National University of Singapore, Kent Ridge, Singapore
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recall BSOn is the classifying space for the special orthogonal group of rank n. It is well known that the mod 2 cohomology ring of BSOn is given as follows:

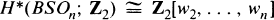
where wi is the i-th mod 2 Stiefel-Whitney class. For the 3-connective cover of BSOn, BSpinn, Quillen in [4] has determined H*(BSpinn) completely for all n. Let BŜOn〈8〉, BŜOn〈16〉 be the classifying spaces for n-plane spin bundle ξ satisfying w4(ξ) = 0 and w4(ξ) = w8(ξ) = 0 respectively. This note follows the method of A. Borel [2] and gives the mod 2 cohomology ring of BŜOn〈8〉 and BŜOn〈16〉 for small n. In particular we answer the question “when is H*(BŜOn〈8〉; Z2), or H*(BŜOn〈16〉; Z2) a polynomial algebra?”

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 5 , 01 October 1985 , pp. 893 - 907
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Adams, J. F., On the non-existence of elements of tlopf invariant one, Ann. of Math. 72 (1960), 20–104.Google Scholar
2. Borel, A., Sur la cohomo/ogie des espaces fibres principau et des espaces homogeneous de groupes de Lie compactes, Ann. of Maths 57 (1953), 115–207.Google Scholar
3. Ng, Tze-Beng, The existence of 7-fields and 8-fields on manifolds, Quart. J. Math. Oxford 30 (1979), 197–221.Google Scholar
4. Quillen, D., The mod 2 cohomology rings of extra-special 2-groups and the spinor groups, Math. Ann. 794 (1971), 197–212.Google Scholar
5. Strong, R. E., Determination of H*(BO(k,…, ∞), Z2) and H*(BU(k, …, ∞), Z2), Trans. Amer. Math. Soc. 107 (1963), 526–544.Google Scholar
6. Wu, W. T., Les i-carrês dans une variété grassmannienne, C. R. Acad. Sci. Paris 230 (1950), 918–920.Google Scholar