No CrossRef data available.
Article contents
A Note on Hyperconvexity in Riemannian Manifolds
Published online by Cambridge University Press: 20 November 2018
Extract
Let M denote a connected Riemannian manifold of class C3, with positive definite C2 metric. The curvature tensor then exists, and is continuous.
By a classical theorem of J. H. C. Whitehead (1), every point x of M has the property that all sufficiently small spherical neighbourhoods V of x are convex; that is, (i) to every y,z ∈ V there is one and only one geodesic segment yz in M which is the shortest path joining them:f:([0, 1]) → M,f(0) = y, f(1) = z; and (ii) this segment yz lies entirely in V:f([0, 1]) 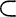 V; (iii) if f is parametrized proportional to arc length, then f(t) is a C2 function of y, t, and z.
V; (iii) if f is parametrized proportional to arc length, then f(t) is a C2 function of y, t, and z.
Let V be a convex set in M; and let y1 y2, Z1, z2 ∈ V.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1959


