Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T08:51:58.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Generalized Witt Algebras

Published online by Cambridge University Press:  20 November 2018

Rimhak Ree
Rimhak Ree*
Affiliation:
The University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this note K will denote a field of characteristic p > 0. Let I be the set {1,2, … , m}, and 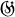a finite additive group of functions on I with values in K. We assume that 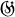is total in the sense that, for any λ1, … , λm in K Σi=imλiσ(i) = 0 for all a in G implies all σi = 0. It is clear that 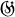is an elementary p-group. Let pn be the order of 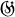. A generalized Witt algebra 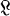is defined as an algebra over K with basis elements {e(σ, i)∣ σ ∈ 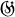, i ∈ I} and the multiplication table

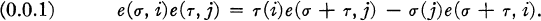
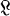is a simple Lie algebra except when p = 2, m = 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 11 , 1959 , pp. 345 - 352
Copyright
Copyright © Canadian Mathematical Society 1959

References

1. Albert, A. A. and Frank, M. S., Simple Lie algebras of characteristic p, Rendiconti del Sem. Mat., Univ. e Politech di Torino, 14 (1955), 117-39.Google Scholar
2. Frank, M. S., A new class of simple Lie algebras, Proc. Nat. Acad. Sci., 40 (1954), 713–18.Google Scholar
3. Jacobson, N., Abstract derivation and Lie algebras, Trans. Amer. Math. Soc, 42 (1937), 206–24.Google Scholar
4. Jennings, S. A. and Ree, Rimhak, On a class of Lie algebras of characteristic p, Trans. Amer. Math. Soc, 84 (1957), 192–207.Google Scholar
5. Ree, Rimhak, On generalized Witt algebras, Trans. Amer. Math. Soc, 83 (1956), 510-46.Google Scholar