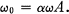A matrix ω having p rows and 2p columns of complex number elements is called a Riemann matrix of genus p if there exists a rational 2p-rowed skew matrix C such that

(1)

is positive definite Hermitian. The matrix C is then called a principal matrix of ω. If ω and ω0 are two Riemann matrices of the same genus, we say that ω and ω0 are isomorphic if there exists a non-singular p-rowed complex matrix α, and a non-singular 2p-rowed rational matrix A, such that

(2)