Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:16:25.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal Completions of Small Categories

Published online by Cambridge University Press:  20 November 2018

J. F. Kennison
J. F. Kennison*
Affiliation:
Clark University, Worcester, Massachusetts
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (3), Isbell proposed a stronger definition for the term “complete category” and obtained many nice theorems for the resulting notion of a completion. In particular, he showed (3, Theorem 3.20) that completions of small categories satisfy a strong normality condition.

In this paper we shall always use the term “complete” in the weaker sense of Freyd (1). (In (3), Isbell used the term “small-complete” for this weaker notion.) We shall prove that the completions, in the sense of Freyd, of small categories also enjoy the same normality condition, provided they admit at least one bicategory structure. (The complete categories in the sense of Isbell always admit bicategory structures; see the remark following Proposition 2.4.)

In what follows, we let mean that 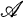is a full subcategory of 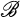. Moreover, if , then 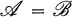means that each object of 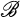is equivalent to an object in .

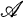Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 196 - 201
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Freyd, P., Abelian categories (Harper and Row, New York, 1964).Google Scholar
2. Isbell, J. R., Some remarks concerning categories and subspaces, Can. J. Math. 9 (1957), 563–577.Google Scholar
3. Isbell, J. R., Structure of categories, Bull. Amer. Math. Soc. 72 (1966), 619–655.Google Scholar
4. Isbell, J. R., Subobjects, adequacy, completeness and categories of algebras, Rozprawy Mat. 34 (1964), 1–33.Google Scholar
5. Kennison, J. F., A note on reflection mappings, Illinois J. Math. 11 (1967), 404–409.Google Scholar
6. Lambek, J., Completions of categories, Lecture Notes in Mathematics, Vol. 24 (Springer- Verlag, Berlin, 1966).Google Scholar