Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T01:15:37.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonvanishing of L-functions, the Ramanujan Conjecture, and Families of Hecke Characters

Published online by Cambridge University Press:  20 November 2018

Valentin Blomer  and
Farrell Brumley
Valentin Blomer
Affiliation:
Universität Göttingen, Mathematisches Institut, Bunsenstr. 3-5, 37073 Göttingen, e-mail: [email protected]
Farrell Brumley
Affiliation:
Institut Galilée, Université Paris 13, 93430 Villetaneuse, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a nonvanishing result for families of 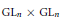$\text{G}{{\text{L}}_{n}}\times \text{G}{{\text{L}}_{n}}$ Rankin–Selberg 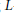$L$-functions in the critical strip, as one factor runs over twists by Hecke characters. As an application, we simplify the proof, due to Luo, Rudnick, and Sarnak, of the best known bounds towards the Generalized Ramanujan Conjecture at the infinite places for cusp forms on 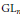$\text{G}{{\text{L}}_{n}}$. A key ingredient is the regularization of the units in residue classes by the use of an Arakelov ray class group.

Keywords

11F7011M41nonvanishingautomorphic formsHecke characters, Ramanujan conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 1 , 01 February 2013 , pp. 22 - 51
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Barthel, L. and Ramakrishnan, D., A nonvanishing result for twists of L-functions of GL(n). Duke Math.J. 74(1994), 681–700. http://dx.doi.org/10.1215/S0012-7094-94-07425-5 Google Scholar
[2]Bergeron, N., Le spectre des surfaces hyperboliques. EDP Sciences, 2011.Google Scholar
[3] Blomer, V. and Brumley, F., On the Ramanujan conjecture over number fields. Ann. of Math. (2) 174(2011), no. 1, 581–605.http://dx.doi.org/10.4007/annals.2011.174.1.18 Google Scholar
[4] Brumley, F., Estimation élémentaire des sommes de Kloosterman multiples. Appendice C of [2].Google Scholar
[5] Booker and, A. R. Krishnamurthy, M., A strengthening of the GL(2) converse theorem. Compos. Math. 147(2011), no. 3, 669–715. http://dx.doi.org/10.1112/S0010437X10005087 Google Scholar
[6] Bruggeman, R.W. and Miatello, R. J., Sum formula for SL2 over a number field and Selberg type estimates for exceptional eigenvalues. Geom. Funct. Anal. 8(1998), 627–655.http://dx.doi.org/10.1007/s000390050069 Google Scholar
[7] Bump, D., Automorphic forms and representations. Cambridge Stud. Adv. Math. 55, Cambridge University Press, 1997.Google Scholar
[8] Clozel, L. and P. Delorme, , Le théorème de Paley-Wiener invariant pour les groupes de Lie r´eductifs. Invent. Math. 77(1984), 427–453. http://dx.doi.org/10.1007/BF01388832 Google Scholar
[9] Cooke, G. and Weinberger, P., On the construction of division chains in algebraic number rings, with applications to SL2. Comm. Algebra 3(1975), 481–524.http://dx.doi.org/10.1080/00927877508822057 Google Scholar
[10] P. Deligne, , Cohomologie étale.SGA 4½ , Lecture Notes in Math. 569, Springer, 1977.Google Scholar
[11] Dimassi, M. and Sjöstrand, J., Spectral asymptotics in the semi-classical limit. London Math. Soc. Lecture Note Ser. 268, Cambridge University Press, Cambridge, 1999.Google Scholar
[12] Duke, W., Number fields with large class group. In: Number theory, CRM Proc. Lecture Notes 36, Amer. Math. Soc., Providence, RI, 2004, 117–126.Google Scholar
[13] Ellenberg, J. and Venkatesh, A., Reflection principles and bounds for class group torsion. Int. Math. Res. Not. IMRN 2007, no. 1.Google Scholar
[14]Iwaniec, H. Luo, ,W. and Sarnak, P., Low lying zeros of families of L-functions. Inst. Hautes ´Etudes Sci. Publ. Math. 91(2000), 55–131.Google Scholar
[15] Iwaniec, H. and Sarnak, P.,Perspectives on the analytic theory of L-functions. In: GAFA 2000 (Tel Aviv, 1999), Geom. Funct. Anal. 2000, Special Volume, Part II, 705–741.Google Scholar
[16] Jacquet, H., Piatetski-Shapiro, I. I. and Shalika, J. A., Rankin–Selberg convolutions. Amer. J. Math 105(1983), 367–464 http://dx.doi.org/10.2307/2374264.Google Scholar
[17]Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations I. Amer. J. Math. 103(1981),499–558.http://dx.doi.org/10.2307/2374103 Google Scholar
[18] Kim, H. and Sarnak, P., Refined estimates towards the Ramanujan and Selberg Conjectures. J. Amer. Math. Soc. 16(2003), 139–183, Appendix to H. Kim, Functoriality for the exterior square of GL(4) and symmetric fourth of GL(2).http://dx.doi.org/10.1090/S0894-0347-02-00410-1 Google Scholar
[19] Krätzel, E., Lattice points. Math. Appl. (East European Ser.) 33, Kluwer Academic Publishers, Dordrecht, 1988.Google Scholar
[20] Landau, E., Über die Anzahl der Gitterpunkte in gewissen Bereichen. Gött. Nachr. 1915, 209–243.Google Scholar
[21] Lenstra, H.W., On Artin's conjecture and Euclid's algorithm in global fields. Invent. Math. 42 (1977), 201–224. http://dx.doi.org/10.1007/BF01389788 Google Scholar
[22] Luo, W., Rudnick, Z. and Sarnak, P., On Selberg's eigenvalue conjecture. Geom. Funct. Anal. 5(1995),387–401. http://dx.doi.org/10.1007/BF01895672 Google Scholar
[23] Luo, W., Rudnick, Z. and Sarnak, P., On the generalized Ramanujan conjecture for GL(n). Proc. Sympos. Pure Math. 66, Part 2, Amer. Math. Soc., Providence, RI, 1999, 301–310.Google Scholar
[24] Michel, Ph. and Venkatesh, A., Heegner points and non-vanishing of Rankin/Selberg L-functions. In: Analytic number theory, Clay Math. Proc. 7, Amer. Math. Soc., Providence, RI, 2007, 169–183.Google Scholar
[25]Montgomery, H. and Weinberger, P., Real quadratic fields with large class number. Math. Ann. 225(1977), 173–176. http://dx.doi.org/10.1007/BF01351721 Google Scholar
[26]Müller, W. and Speh, B., Absolute convergence of the spectral side of the Arthur trace formula for GLn. With an appendix by E. M. Lapid. Geom. Funct. Anal. 14(2004),58–93. http://dx.doi.org/10.1007/s00039-004-0452-0 Google Scholar
[27]R. A. Rankin, , Contributions to the theory of Ramanujan's function T(n) and similar arithmetical functions. II. The order of the Fourier coefficients of integral modular forms. Proc. Cambridge Philos. Soc. 35(1939), 351–372; III. A note on the sum function of the Fourier coefficients of integral modular forms. Proc. Cambridge Philos. Soc. 36(1940), 150-151. http://dx.doi.org/10.1017/S0305004100017114 Google Scholar
[28] Rohrlich, D., Nonvanishing of L-functions for GL(2). Invent. Math. 97(1989), 383–401. http://dx.doi.org/10.1007/BF01389047 Google Scholar
[29]Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory. Duke Math. J. 81(1996), 269–322. http://dx.doi.org/10.1215/S0012-7094-96-08115-6 Google Scholar
[30]Sarnak, P., Fourth moments of Gr¨ossencharakteren zeta functions. Comm. Pure Appl. Math. 38(1985), 167–178. http://dx.doi.org/10.1002/cpa.3160380204 Google Scholar
[31]Sarnak, P., Families of L-functions. Preprint.Google Scholar
[32] R.|Schoof, Arakelov class groups. Lecture notes, by J. Voight, available from http://websites.math.leidenuniv.nl/algebra.Google Scholar
[33]Serre, J.-P., Letter to J.-M. Deshouillers, 1981.Google Scholar
[34] Weil, A., Basic Number Theory. Springer-Verlag, New York, 1967.Google Scholar