Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:21:51.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Selfadjoint Perturbations of Selfadjoint Operators in Two Dimensions IIIa. One Branching Point

Published online by Cambridge University Press:  20 November 2018

Michael Hitrik  and
Johannes Sjöstrand
Michael Hitrik
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095-1555, U.S.A. e-mail:, [email protected]
Johannes Sjöstrand
Affiliation:
Centre de Mathématiques, École Polytechnique, FR 91128 Palaiseau France e-mail:, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

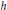This is the third in a series of works devoted to spectral asymptotics for non-selfadjoint perturbations of selfadjoint $h$-pseudodifferential operators in dimension 2, having a periodic classical flow. Assuming that the strength $\epsilon$ of the perturbation is in the range 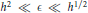${{h}^{2}}\ll \epsilon \ll {{h}^{1/2}}$ (and may sometimes reach even smaller values), we get an asymptotic description of the eigenvalues in rectangles 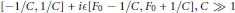$[-1/C,1/C]+i\epsilon [{{F}_{0}}-1/C,{{F}_{0}}+1/C],C\gg 1$, when 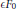$\epsilon {{F}_{0}}$ is a saddle point value of the flow average of the leading perturbation.

Keywords

31C1035P2035Q4037J3537J4553D2258J40non-selfadjointeigenvalueperiodic flowbranching singularity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 572 - 657
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Beraha, S., Kahane, J., and Weiss, N. J., Limits of zeros of recursively defined families of polynomials. In: Studies in Foundations and Combinatorics. Adv. in Math. Suppl. Stud. 1, Academic Press, New York, 1978, pp. 213–232, .Google Scholar
[2] Boutet, L. de Monvel and Krée, P. Pseudo-differential operators and Gevrey classes. Ann. Inst. Fourier (Grenoble) 17(1967), 295–323.Google Scholar
[3] Colin, Y. de Verdière and Parisse, B., équilibre instable en régime semi-classique. II. Conditions de Bohr-Sommerfeld, Ann. Inst. H. Poincaré Phys. Théor. 61(1994), no. 3, 347–367.Google Scholar
[4] Colin, Y. de Verdière and V˜u Ngo, S.. c, Singular Bohr-Sommerfeld rules for 2D integrable systems. Annales Sci. école Norm. Sup. 36(2003), 1–55.Google Scholar
[5] Combescure, M., Ralston, J., and Robert, D., A proof of the Gutzwiller semiclassical trace formula using coherent states decomposition. Comm. Math. Phys. 202(1999), no. 2, 463–480.Google Scholar
[6] Dacorogna, B. and Moser, J., On a partial differential equation involving the Jacobian determinant. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 7(1990), no. 1, 1–26.Google Scholar
[7] Davies, E. B., Eigenvalues of an elliptic system, Math. Z. 243(2003), no. 4, 719–743.Google Scholar
[8] Davies, E. B., Non-self-adjoint differential operators. Bull. LondonMath. Soc. 34(2002), no. 5, 513–532.Google Scholar
[9] Dencker, N., Sjöstrand, J., and Zworski, M., Pseudospectra of semiclassical (pseudo-) differential operators. Comm. Pure Appl. Math. 57(2004), no. 3, 384–415.Google Scholar
[10] Fujiié, S. and Ramond, T.,Matrice de scattering et résonances associées à une orbite hétérocline. Ann. Inst. H. Poincaré Phys. Théor. 69(1998), no. 1, 31–82.Google Scholar
[11] Hager, M., Instabilité spectrale semiclassique pour des opérateurs non-autoadjoints. I. un modèle. Ann. Fac. Sci. Toulouse Math. 15(2006), no. 2, 243–280.Google Scholar
[12] Helffer, B. and Sjöstrand, J., Résonances en limite semiclassique. Mém. Soc. Math. France (N.S.) no. 24-25, 1986.Google Scholar
[13] Helffer, B. and Sjöstrand, J., Semiclassical analysis for Harper's equation. III. Cantor structure of the spectrum. Mem. Soc. Math. France (N.S.) no. 39, 1989, 1–124.Google Scholar
[14] Hitrik, M., and Sjöstrand, J., Non-selfadjoint perturbations of selfadjoint operators in 2 dimensions. I. Ann. Henri Poincaré 5(2004), no. 1, 1–73.Google Scholar
[15] Hitrik, M., and Sjöstrand, J., Non-selfadjoint perturbations of selfadjoint operators in 2 dimensions. II. Vanishing averages. Comm. Partial Differential Equations 30(2005), no. 7-9, 1065–1106.Google Scholar
[16] Hitrik, M., Sjöstrand, J., and V˜u Ngo, S.. c, Diophantine tori and spectral asymptotics for nonselfadjoint operators. Amer. J. Math. 129(2007), no. 1, 105–182.Google Scholar
[17] Melin, A. and Sjöstrand, J., Determinants of pseudodifferential operators and complex deformations of phase space. Methods Appl. Anal. 9(2002), no. 2, 177–237.Google Scholar
[18] Melin, A. and Sjöstrand, J., Bohr-Sommerfeld quantization condition for non-selfadjoint operators in dimension 2, Astérisque No. 284 (2003), 181–244.Google Scholar
[19] Nedelec, L., Perturbations of non self-adjoint Sturm-Liouville problems, with applications to harmonic oscillators. Methods Appl. Anal. 13(2006), no. 1, 123–148.Google Scholar
[20] Olver, F. W., Asymptotics and Special Functions, Computer Science and Applied Mathematics. Academic Press, New York, 1974.Google Scholar
[21] Ramond, T., Semiclassical study of quantum scattering on the line. Comm. Math. Phys. 177(1996), no. 1, 221–254.Google Scholar
[22] Redparth, P., Spectral properties of non-self-adjoint operators in the semi-classical regime, J. Differential Equations 177(2001), no. 2, 307–330.Google Scholar
[23] Servat, E. and Tovbis, A., On the Zakharov-Shabat problem. http://www.math.univ-paris13.fr/˜amar/ Google Scholar
[24] Shkalikov, A. A., Spectral properties of the Orr-Sommerfeld operator with large Reynolds numbers. J. Math. Sci. (N.Y.) 124(2004), no. 6, 5417–5441.Google Scholar
[25] Siburg, K. F., Symplectic capacities in two dimensions. Manuscripta Math. 78(1993), no. 2, 149–163.Google Scholar
[26] Sjöstrand, J., Singularités analytiques microlocales. Astérisque 95, 1982.Google Scholar
[27] Sjöstrand, J., Density of resonances for strictly convex analytic obstacles. Canad. J. Math. 48(1996), no. 2, 397–447.Google Scholar
[28] Sjöstrand, J., Resonances for bottles and trace formulae, Math. Nachr. 221(2001), 95–149.Google Scholar
[29] Sjöstrand, J., Perturbations of selfadjoint operators with periodic classical flow, In: Wave Phenomena and Asymptotic Analysis. RIMS Kokyuroku 1315, April 2003. See also www.arxiv.org/abs/math.SP/0303023.Google Scholar
[30] Sjöstrand, J., Resonances associated to a closed hyperbolic trajectory in dimension 2. Asymptot. Anal. 36(2003), no. 2, 93–113.Google Scholar
[31] Sjöstrand, J. and Zworski, M., Quantum monodromy and semi-classical trace formulae. J.Math. Pures Appl. 81(2002), no. 1, 1–33.Google Scholar
[32] Trefethen, L. N., Spectral Methods in Matlab. SIAM, Philadelphia, PA, 2000.Google Scholar