Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:00:30.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonnegative Solutions for Weakly Nonlinear Elliptic Equations

Published online by Cambridge University Press:  20 November 2018

Walter Allegretto
Walter Allegretto*
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let x = (x1, … xn) denote a point of Euclidean n space En and set Di = ∂/∂xi for i = 1, … n. Let Ω denote an exterior domain in En with smooth boundary and consider in Ω the formal elliptic problem:

1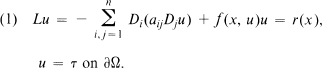

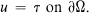
We first consider the problem of finding nonnegative generalized solutions of (1) when τ ≧ 0, τ ≢ 0, and r(x) ≡ 0. Under more stringent conditions on the coefficients and for suitable r(x), we then show the existence of a locally bounded solution. Next, we show that, under stronger assumptions, our main criterion is also necessary. The final arguments are devoted to the consideration of illustrative examples.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 1 , 01 February 1984 , pp. 71 - 83
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Allegretto, W., Positive solutions and spectral properties of second order elliptic operators, Pacific J. Math. 92 (1981), 15–25.Google Scholar
2. Allegretto, W., Positive solutions of elliptic equations in unbounded domains, J. Math. Anal. Appl. 54 (1981), 372–380.Google Scholar
3. Ako, K. and Kusano, T., On bounded solutions of second order elliptic differential equations, J. Fac. Sci. Univ. Tokyo 11 (1964), 29–37.Google Scholar
4. Amann, H., On the existence of positive solutions of nonlinear elliptic boundary value problems, Indiana Univ. Math. J. 21 (1971), 125–146.Google Scholar
5. Amann, H., Supersolutions, monotone iterations and stability, J. Differential Equations 21 (1976), 363–377.Google Scholar
6. Amann, H. and Crandall, M., On some existence theorems for semi-linear elliptic equations, Indiana Univ. Math. J. 27 (1978), 779–790.Google Scholar
7. Aubin, T., Problems isoperimetriques et espaces de Sobolev, C. R. Acad. Sci. Paris 280 (1975), 279–281.Google Scholar
8. Berestycki, H. and Lions, P. L., Une methode locale pour l'existence de solutions positives de problemes semi lineaires elliptiques dans Rn, J. Analyse Math. 38 (1980), 144–187.Google Scholar
9. Cac, N. P., Nonlinear elliptic boundary value problems for unbounded domains, J. Differential Equations 45 (1982), 191–198.Google Scholar
10. Deuel, J. and Hess, P., A criterion for the existence of solutions of nonlinear elliptic boundary value problems, Proc. Roy. Soc. Edinburgh 74A (1974), 49–54.Google Scholar
11. Donato, P., Migliaccio, L. and Schianchi, R., Semilinear elliptic equations in unbounded domains of Rn, Proc. Roy. Soc. Edinburgh 88A (1981), 109–119.Google Scholar
12. Edmunds, D., Moscatelli, V. and Webb, J., Operateurs elliptiques fortement non linéaires dans les domaines non bornes, C. R. Acad. Se. Paris 278 (1974), 1505–1508.Google Scholar
13. Friedman, A., Partial differential equations (Holt, Rinehart and Winston, New York, 1969).Google Scholar
14. Fucik, S., Solvability of nonlinear equations and boundary value problems (D. Riedel, Boston, 1980).Google Scholar
15. Furusho, Y. and Ogura, Y., On the existence of bounded positive solutions of semilinear elliptic equations in exterior domains, Duke Math. J. 48 (1981), 497–521.Google Scholar
16. Gidas, B. and Spruck, J., Global and local behavior of positive solutions of nonlinear elliptic equations, Comm. Pure Appl. Math. 34 (1981), 525–598.Google Scholar
17. Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order (Springer, Verlag, Berlin, 1977).CrossRefGoogle Scholar
18. Hess, P., On the solvability of nonlinear elliptic boundary value problems, Indiana Univ. Math J. 25 (1976), 461–466.Google Scholar
19. Hess, P., On a class of strongly nonlinear elliptic variational inequalities, Math. Ann. 211 (1974), 289–297.Google Scholar
20. Hess, P., On a second-order nonlinear elliptic boundary value problem (Nonlinear Analysis, Academic Press, New York, 1978), 99–107.Google Scholar
21. Kazdan, J. and Kramer, R., Invariant criteria for existence of solutions to second order quasi linear elliptic equations, Comm. Pure Appl. Math. 31 (1978), 619–645.Google Scholar
22. Kazdan, J. and Warner, F., Remarks on some quasilinear elliptic equations, Comm. Pure Appl. Math. 28 (1975), 567–597.Google Scholar
23. Kramer, R., Sub- and super-solutions of quasi linear elliptic boundary value problems, J. Differential Equations 28 (1978), 278–283.Google Scholar
24. Noussair, E., On semi linear elliptic boundary value problems in unbounded domains, J. Differential Equations 41 (1981), 334–348.Google Scholar
25. Ogata, A., On bounded positive solutions of nonlinear elliptic boundary value problems in an exterior domain, Funkciol. Ekvoc. 17 (1974), 207–222.Google Scholar
26. Pokhozaev, S. I., On equations of the form Δu = f(x, u, Du), Math. U. S. S. R. Sbornik 41 (1982), 269–280.Google Scholar
27. Swanson, C. A., Bounded positive solutions of semi linear Schrodinger equations, SIAM J. Math Anal. 13 (1982), 40–47.Google Scholar
28. Talenti, G., Best constant in Sobolev inequality, Ann. Mat. Pura Appl. 110 (1976), 353–372.Google Scholar