Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T08:30:45.864Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Existence of Ramanujan Congruences in Modular Forms of Level Four

Published online by Cambridge University Press:  20 November 2018

Michael Dewar
Michael Dewar*
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Kingston, ON email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

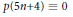Ramanujan famously found congruences like $p(5n\,+\,4)\,\equiv \,0$ mod 5 for the partition function. We provide a method to find all simple congruences of this type in the coefficients of the inverse of a modular form on 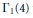${{\Gamma }_{1}}(4)$ that is non-vanishing on the upper half plane. This is applied to answer open questions about the (non)-existence of congruences in the generating functions for overpartitions, crank differences, and 2-colored 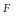$F$-partitions.

Keywords

11F3311P83modular formRamanujan congruencegeneralized Frobenius partitionoverpartitioncrank
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 6 , 01 December 2011 , pp. 1284 - 1306
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Ahlgren, S. and M. Boylan, Arithmetic properties of the partition function. Invent. Math. 153(2003), no. 3, 487–502. doi:10.1007/s00222-003-0295-6Google Scholar
[2] Ahlgren, S., D. Choi, and J. Rouse, Congruences for level four cusp forms. Math. Res. Lett. 16(2009), no. 4, 683–701.Google Scholar
[3] Andrews, G. E., Generalized Frobenius partitions. Mem. Amer. Math. Soc. 49(1984), 1–44.Google Scholar
[4] L, A. O.. Atkin and F. G. Garvan, Relations between the ranks and cranks of partitions. Ramanujan J. 7(2003), no. 1–3, 343–366. doi:10.1023/A:1026219901284Google Scholar
[5] Boylan, M., Exceptional congruences for powers of the partition function. Acta Arith. 111(2004), no. 2, 187–203. doi:10.4064/aa111-2-7Google Scholar
[6] Choi, D., S.-Y. Kang, and J. Lovejoy, Partitions weighted by the parity of the crank. J. Combin. Theory Ser. A 116(2009), no. 5, 1034–1046. doi:10.1016/j.jcta.2009.02.002Google Scholar
[7] Corteel, S. and J. Lovejoy, Overpartitions. Trans. Amer. Math. Soc. 356(2004), no. 4, 1623–1635. doi:10.1090/S0002-9947-03-03328-2Google Scholar
[8] Eichhorn, D. and J. A. Sellers, Computational proofs of congruences for 2-colored Frobenius partitions. Int. J. Math. Math. Sci. 29(2002), no. 6, 333–340. doi:10.1155/S0161171202007342Google Scholar
[9] Gross, B. H., A tameness criterion for Galois representations associated to modular forms (mod p). Duke Math. J. 61(1990), no. 2, 445–517. doi:10.1215/S0012-7094-90-06119-8Google Scholar
[10] Jochnowitz, N., A study of the local components of the Hecke algebra mod l. Trans. Amer. Math. Soc. 270(1982), no. 1, 253–267.Google Scholar
[11] Kim, B., The overpartition function modulo 128. Integers 8(2008), A38, 1–8.Google Scholar
[12] Kiming, I. and J. B. Olsson, Congruences like Ramanujan's for powers of the partition function. Arch. Math. (Basel) 59(1992), no. 4, 348–360.Google Scholar
[13] Lovejoy, J., Ramanujan-type congruences for three colored Frobenius partitions. J. Number Theory 85(2000), no. 2, 283–290. doi:10.1006/jnth.2000.2546Google Scholar
[14] Mahlburg, K., Partition congruences and the Andrews-Garvan-Dyson crank. Proc. Natl. Acad. Sci. USA 102(2005), no. 43, 15373–15376. doi:10.1073/pnas.0506702102Google Scholar
[15] Mahlburg, K., The overpartition function modulo small powers of 2. Discrete Math. 286(2004), no. 3, 263–267. doi:10.1016/j.disc.2004.03.014Google Scholar
[16] Ono, K., The web of modularity: arithmetic of the coefficients of modular forms and q-series. CBMS Regional Conference Series in Mathematics, 102, Conference Board of the Mathematical Sciences, Washington, DC; American Mathematical Society, Providence, RI, 2004.Google Scholar
[17] Ono, K., Distribution of the partition function modulo m. Ann. of Math. (2) 151(2000), no. 1, 293–307. doi:10.2307/121118Google Scholar
[18] Ono, K., Congruences for Frobenius partitions. J. Number Theory 57(1996), no. 1, 170–180. doi:10.1006/jnth.1996.0041Google Scholar
[19] Paule, P. and S. Radu, A proof of Seller's conjecture. RISC. Technical report no. 09-17, 2009.Google Scholar
[20] Sinick, J., Ramanujan Congruences for a class of eta quotients. Int. J. Number Theory 6(2010), no. 4, 835–847.Google Scholar
[21] Sturm, J.. On the congruence of modular forms. In: Number theory (New York, 1984–1985), Lecture Notes in Math., 1240, Springer, Berlin, 1987, pp. 275–280.Google Scholar
[22] F, H. P.. Swinnerton-Dyer, On l-adic representations and congruences for coefficients of modular forms. In: Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, 1972), Lecture Notes in Math., 350, Springer, Berlin, 1973, pp. 1–55.Google Scholar
[23] Tupan, A., Congruences for 1(4)-modular forms of half-integral weight. Ramanujan J. 11(2006), no. 2, 165–173. doi:10.1007/s11139-006-6505-2Google Scholar