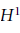Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T02:27:53.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonabelian ${{H}^{1}}$ and the Étale Van Kampen Theorem

Published online by Cambridge University Press:  20 November 2018

Michael D. Misamore
Michael D. Misamore*
Affiliation:
Universität Duisburg-Essen, Universitätsstr. 2, 45141 Essen, Germany email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Generalized étale homotopy pro-groups $\pi _{1}^{\acute{e}t}(C, x)$ associated with pointed, connected, small Grothendieck sites 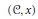$(C, x)$ are defined, and their relationship to Galois theory and the theory of pointed torsors for discrete groups is explained.

Applications include new rigorous proofs of some folklore results around 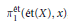$\pi _{1}^{\acute{e}t}(\acute{e}t(X) x)$, a description of Grothendieck's short exact sequence for Galois descent in terms of pointed torsor trivializations, and a new étale van Kampen theorem that gives a simple statement about a pushout square of pro-groups that works for covering families that do not necessarily consist exclusively of monomorphisms. A corresponding van Kampen result for Grothendieck's profinite groups 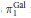$\text{ }\!\!\pi\!\!\text{ }_{1}^{\text{Gal}}$ immediately follows.

Keywords

18G3014F35étale homotopy theorysimplicial sheaves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 6 , 01 December 2011 , pp. 1388 - 1415
Copyright
Copyright © Canadian Mathematical Society 2011

References

[AM69] Artin, M. and B. Mazur, Étale homotopy. Lecture Notes in Mathematics, 100, Springer-Verlag, Berlin-New York, 1969.Google Scholar
[Dub04] Dubuc, E. J., On the representation theory of Galois and atomic topoi. J. Pure Appl. Algebra 186(2004), no. 3, 233–275. doi:10.1016/S0022-4049(03)00141-5Google Scholar
[Fri82] Friedlander, E. M., Étale homotopy of simplicial schemes. Annals of Mathematics Studies, 104, Princeton University Press, Princeton, NJ, 1982.Google Scholar
[GJ99] Goerss, P. G. and J. F. Jardine, Simplicial homotopy theory. Progress in Mathematics, 174, Birkhäuser Verlag, Basel, 1999.Google Scholar
[Jar86] Jardine, J. F., Simplicial objects in a Grothendieck topos. In: Applications of algebraic K-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., 55, American Mathematical Society, Providence, RI, 1986, pp. 193–239.Google Scholar
[Jar87] Jardine, J. F., Simplicial presheaves. J. Pure Appl. Algebra 47(1987), no. 1, 35–87. doi:10.1016/0022-4049(87)90100-9Google Scholar
[Jar89] Jardine, J. F., Universal Hasse-Witt classes. In: Algebraic K-theory and algebraic number theory (Honolulu, HI, 1987), Contemp. Math., 83, American Mathematical Society, Providence, RI, 1989, pp. 83–100.Google Scholar
[Jar94] Jardine, J. F., Higher spinor classes. Mem. Amer. Math. Soc. 110(1994), no. 528. [Jar06] , Torsors and stacks. Mediterr. J. Math. 3(2006), no. 2, 251–258. doi:10.1007/s00009-006-0075-9Google Scholar
[Jar09a] Jardine, J. F., Cocycle categories. In: Algebraic Topology, Abel Symp., 4, Springer, Berlin, 2009, pp. 185–219.Google Scholar
[Jar09b] , Pointed torsors. Preprint, http://www.math.uwo.ca/_jardine/papers/preprints/pointed-2010.pdf.Google Scholar
[Jar09c] Jardine, J. F., The Verdier hypercovering theorem. Preprint, http://www.math.uwo.ca/_jardine/papers/preprints/Verdier4.pdf.Google Scholar
[Moe89] Moerdijk, I., Prodiscrete groups and Galois toposes. Nederl. Akad.Wetensch. Indag. Math. 51(1989), no. 2, 219–234.Google Scholar
[Moe95] Moerdijk, I., Classifying spaces and classifying topoi. Lecture Notes in Mathematics, 1616, Springer-Verlag, Berlin, 1995.Google Scholar
[Noo04] Noohi, B., Fundamental groups of algebraic stacks. J. Inst.Math. Jussieu 3(2004), no. 1, 69–103. doi:10.1017/S1474748004000039Google Scholar
[Ser94] Serre, J.-P., Cohomologie Galoisienne, Fifth ed., Lecture Notes in Mathematics, vol. 5, Springer-Verlag, Berlin, 1994.Google Scholar
[SGA70] SGA 3, schémas en groupes, 1962-1964, Lecture Notes in Mathematics, 151, 152, 153, Springer, Berlin, 1970.Google Scholar
[SGA72] SGA 4, Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. Springer-Verlag, Berlin, 1972, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964, Dirigé par M. Artin, A. Grothendieck, et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat, Lecture Notes in Mathematics, 269, Springer-Verlag, Berlin-New York, 1972.Google Scholar
[SGA03] SGA 1, Revêtements étales et groupe fondamental (SGA 1). Séminaire de géométrie algébrique du Bois Marie 1960–61. Directed by A. Grothendieck,With two papers by M. Raynaud, Updated and annotated reprint of the 1971 original [Lecture Notes in Math., 224, Springer, Berlin], Documents Mathématiques (Paris), 3, Société Mathématique de France, Paris, 2003. [Sti06] J. Stix, A general Seifert-Van Kampen theorem for algebraic fundamental groups. Publ. Res. Inst. Math. Sci. 42(2006), no. 3, 763–786. doi:10.2977/prims/1166642159Google Scholar
[Zoo01] Zoonekynd, V., The fundamental group of an algebraic stack. 2001. arxiv:math/0111071v1Google Scholar
[Zoo02] Zoonekynd, V., Théorème de van Kampen pour les champs algébriques. Ann. Math. Blaise Pascal 9(2002), no. 1, 101–145.Google Scholar