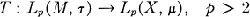Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:53:55.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Non Commutative Lp Spaces II

Published online by Cambridge University Press:  20 November 2018

A. Katavolos
A. Katavolos*
Affiliation:
University of Athens, Panepistimiopolis, Athens, Greece
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a w*-algebra (Von Neumann algebra), τ a semifinite, faithful, normal trace on M. There exists a w*-dense (i.e., dense in the σ(M, M*)-topology, where M* is the predual of M) *-ideal J of M such that τ is a linear functional on J, and

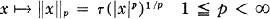
(where |x| = (x*x)1/2) is a norm on J. The completion of J in this norm is Lp(M, τ) (see [2], [8], [7], and [4]).

If M is abelian, in which case there exists a measure space (X, μ) such that M = L∞(X, μ), then Lp(X, τ) is isometric, in a natural way, to Lp(X, μ). A natural question to ask is whether this situation persists if M is non-abelian. In a previous paper [5] it was shown that it is not possible to have a linear mapping

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 5 , 01 October 1982 , pp. 1208 - 1214
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Broise, M., Sur les isomorphismes de certaines algèbres de Von Neumann, Ann. Sci. Ec. Norm. Sup. 83, 3me série (1966), 91–111./Google Scholar
2. Dixmier, J., Formes linéaires sur un anneau d'opérateurs, Bull. Soc. Math. Fr. 81 (1953), 9–39./Google Scholar
3. Dixmier, J., Les algèbres d’ opérateurs dans l'espace hilbertien, 2me édition (Gauthier-Villars, Paris, 1969)./Google Scholar
4. Katavolos, A., Ph.D. Dissertation, Univ. of London (1977)./Google Scholar
5. Katavolos, A., Are non-commutative Lp spaces really non-commutative? Can. J. Math. 33 (1981), 1319–1327./Google Scholar
6. Lamperti, J., On the isometries of certain function spaces, Pacific J. Math. 8 (1958), 459–466./Google Scholar
7. Nelson, E., Notes on non-commutative intergration, J. Funct. Anal. 15 (1974), 103–116./Google Scholar
8. Segal, I. E., A non-commutative extension of abstract intergration, Ann. Math. 57 (1953), 401–457./Google Scholar