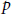Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-26T03:21:00.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent Conjugacy Classes in $p$-adic Lie Algebras: The Odd Orthogonal Case

Published online by Cambridge University Press:  20 November 2018

Jyotsna Mainkar Diwadkar
Jyotsna Mainkar Diwadkar*
Affiliation:
Department of Mathematics, University of Pittsburgh, Pittsburgh, PA 15260, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will study the following question: Are nilpotent conjugacy classes of reductive Lie algebras over 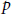$p$-adic fields definable? By definable, we mean definable by a formula in Pas's language. In this language, there are no field extensions and no uniformisers. Using Waldspurger's parametrization, we answer in the affirmative in the case of special orthogonal Lie algebras 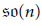$\mathfrak{s}\mathfrak{o}\left( n \right)$ for 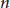$n$ odd, over 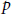$p$-adic fields.

Keywords

17B1003C60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 88 - 108
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Denef, J. and Loeser, F., Definable sets, motives and p-adic integrals. J. Amer.Math. Soc. 14(2001), no. 2, 429–469.Google Scholar
[2] Gordon, J.: Motivic nature of character values of depth-zero representations. Int. Math. Rev. Not 2004, no. 34, 1735–1760.Google Scholar
[3] Gordon, J. and Hales, T. C., Virtual Transfer Factors arXiv:math.RT/0209001 2002.Google Scholar
[4] Enderton, H. B., A mathematical introduction to logic. Second edition. Harcourt Academic Press, Burlington,MA, 2001.Google Scholar
[5] Hales, T. C., Can p-adic integrals be computed? arXiv:math.RT/0205207, 2002.Google Scholar
[6] Hales, T. C., Orbital integrals are motivic arXiv:math.RT/0212236, 2002.Google Scholar
[7] Hodges, W. A Shorter Model Theory. Cambridge University Press, Cambridge, 1997.Google Scholar
[8] Iwasawa, K.: Local Class Field Theory. Oxford University Press. New York, 1986.Google Scholar
[9] O’Meara, O. T.: Introduction to Quadratic Forms. Grundlehren des Mathematischen Wissenschaften 117, Springer-Verlag, Berlin, 1963.Google Scholar
[10] Pas, J.: Uniform p-adic cell decomposition and local zeta functions. J. Reine Angew.Math. 399(1989), 137–172.Google Scholar
[11] Quine, W. V., Mathematical Logic. Revised edition. Harvard University Press, Cambridge, MA, 1981.Google Scholar
[12] Quine, W. V., Set Theory and Its Logic. Harvard University Press, Cambridge, MA, 1963.Google Scholar
[13] Repka, J.: Shalika's Germs for p-adic GL(n). I. II. Pacific J. Math. 113(1984), no. 1, 165–182.Google Scholar
[14] Scharlau, W., Quadratic and Hermitian Forms. Grundlehren derMathematischenWissenschaften 270, Springer-Verlag, Berlin, 1985.Google Scholar
[15] Serre, Jean-Pierre, A Course in Arithmetic. Graduate Texts in Mathematics 7, Springer-Verlag, Berlin, 1973.Google Scholar
[16] Shalika, J. A., A theorem on semi-simple p-adic groups. Ann. of Math. 95(1972), 226–242.Google Scholar
[17] Waldspurger, J.-L., Intégrales orbitales nilpotentes et endoscopic pour les groupes classiques non ramifiés. Astérisque no. 269, 2001 Google Scholar