Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T21:01:28.814Z Has data issue: false hasContentIssue false
  • English
  • Français

A new approach to weak convergence of random cones and polytopes

Part of: General convexity Geometric probability and stochastic geometry Polytopes and polyhedra Limit theorems

Published online by Cambridge University Press:  11 August 2020

Zakhar Kabluchko ,
Daniel Temesvari  and
Christoph Thäle
Zakhar Kabluchko
Affiliation:
Institut für Mathematische Stochastik, Westfälische Wilhelms-Universität Münster, Münster, Germany e-mail: [email protected]
Daniel Temesvari
Affiliation:
Institut für Diskrete Mathematik und Geometrie, Technische Universität Wien, Wien, Austria e-mail: [email protected]
Christoph Thäle*
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Bochum, Germany
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A new approach to prove weak convergence of random polytopes on the space of compact convex sets is presented. 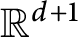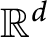This is used to show that the profile of the rescaled Schläfli random cone of a random conical tessellation, generated by n independent and uniformly distributed random linear hyperplanes in $\mathbb {R}^{d+1}$ , weakly converges to the typical cell of a stationary and isotropic Poisson hyperplane tessellation in $\mathbb {R}^d$ , as 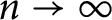$n\to \infty $ .

Keywords

Cover–Efron conerandom conerandom polytoperandom tessellationScheffé’s lemmaSchläfli conestochastic geometrytypical cellweak convergence

MSC classification

Primary: 52A22: Random convex sets and integral geometry
Secondary: 60D05: Geometric probability and stochastic geometry 52A55: Spherical and hyperbolic convexity 52B11: $n$-dimensional polytopes 60F05: Central limit and other weak theorems
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 6 , December 2021 , pp. 1627 - 1647
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Z.K. has been supported by the German Research Foundation under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics–Geometry–Structure.

References

Amelunxen, D. and Lotz, M., Intrinsic volumes of polyhedral cones: a combinatorial perspective . Discrete Comput. Geom. 58(2017), 371–409.CrossRefGoogle Scholar
Amelunxen, D. and Bürgisser, P., Intrinsic volumes of symmetric cones and applications in convex programming . Math. Program. Ser. A 149(2015), 105–130.CrossRefGoogle Scholar
Amelunxen, D., Lotz, M., McCoy, M. B., and Tropp, J. A., Living on the edge: phase transitions in convex programs with random data . Inf. Inference J IMA 3(2014), 224–298.CrossRefGoogle Scholar
Arbeiter, E. and Zähle, M., Geometric measures for random mosaics in spherical spaces . Stoch. Stoch. Rep. 46(1994), 63–77.CrossRefGoogle Scholar
Bárány, I., Random polytopes, convex bodies, and approximation . In: Weil, W. (ed.), Stochastic geometry, Lecture Notes Math, Springer, New York, 2007, p. 1892.Google Scholar
Bárány, I., Hug, D., Reitzner, M., and Schneider, R., Random points in halfspheres . Random Struct. Algor. 50(2017), 3–22.CrossRefGoogle Scholar
Bárány, I. and Thäle, C., Intrinsic volumes and Gaussian polytopes: the missing piece of the jigsaw . Doc. Math. 22(2017), 1323–1335.Google Scholar
Bárány, I. and Vu, V. H., Central limit theorems for Gaussian polytopes . Ann. Probab. 35(2007), 1593–1621.CrossRefGoogle Scholar
Billingsley, P., Convergence of probability measures. 2nd ed., Wiley Series in Probability and Statistics, John Wiley & Sons, Inc., Hoboken, NJ, 1999.CrossRefGoogle Scholar
Cohn, D. L., Measure theory. Birkhäuser, Basel, 1980.CrossRefGoogle Scholar
Cover, T. M. and Efron, B., Geometrical probability and random points on a hypersphere . Ann. Math. Stat. 38(1967), 213–220.CrossRefGoogle Scholar
Durrett, R., Probability—theory and examples . 4th ed., Cambridge University Press, Cambridge, UK, 2010.CrossRefGoogle Scholar
Goldstein, L., Nourdin, I., and Peccati, G., Gaussian phase transitions and conic intrinsic volumes: Steining the Steiner formula . Ann. Appl. Probab. 27(2017), 1–47.CrossRefGoogle Scholar
Hug, D., Random polytopes . In: Spodarev, E. (ed.), Stochastic geometry, spatial statistics and random fields. Asymptotic methods, Lecture Notes Mathematics, 2068, Springer-Verlag, New York, 2013.Google Scholar
Hug, D. and Schneider, R., Random conical tessellations . Discrete Comput. Geom. 56(2016), 395–426.CrossRefGoogle Scholar
Hug, D. and Thäle, C., Splitting tessellations in spherical spaces . Electron. J. Probab. 24(2019), article 24, 60 pp.CrossRefGoogle Scholar
Kabluchko, Z., Expected $f$ -vector of the Poisson zero polytope and random convex hulls in the half-sphere. Mathematika, 66(2020), 1028–1053.CrossRefGoogle Scholar
Kabluchko, Z., Angles of random simplices and face numbers of random polytopes. Preprint, 2020. arXiv:1909.13335CrossRefGoogle Scholar
Kabluchko, Z., Marynych, A., Temesvari, D., and Thäle, C., Cones generated by random points on half-spheres and convex hulls of Poisson point processes . Probab. Theory Related Fields 175(2019), 1021–1061.CrossRefGoogle Scholar
Kabluchko, Z., Temesvari, D., and Thäle, C., Expected intrinsic volumes and facet numbers of random beta-polytopes . Math. Nachr. 292(2019), 79–105.CrossRefGoogle Scholar
Kabluchko, Z. and Thäle, C., The typical cell of a Voronoi tessellation on the sphere. Preprint, 2020. arXiv:1911.07221CrossRefGoogle Scholar
Kabluchko, Z., Thäle, C., and Zaporozhets, D., Beta polytopes and Poisson polyhedra: $f$ -vectors and angles . Adv. Math. 374(2020), 107333.CrossRefGoogle Scholar
Kingman, J. F. C., Poisson processes, Oxford University Press, Oxford, UK, 1993.Google Scholar
McCoy, M. B. and Tropp, J. A., From Steiner formulas for cones to concentration of intrinsic volumes . Discrete Comput. Geom. 51(2014), 926–963.CrossRefGoogle Scholar
Miles, R. E., Random points, sets and tessellations on the surface of a sphere . Sankhya Ser. A 33(1971), 145–174.Google Scholar
Moszyńska, M., Selected topics in convex geometry. Birkhäuser, Basel, 2006.Google Scholar
Reitzner, M., Central limit theorems for random polytopes . Probab. Theory Relat. Fields 133(2005), 483–507.CrossRefGoogle Scholar
Reitzner, M., Random polytopes . In: Molchanov, I. and Kendall, W. (eds.), New perspectives in stochastic geometry, Oxford University Press, Oxford, UK, 2010.Google Scholar
Rényi, A. and Sulanke, R., Über die konvexe Hülle von $n$ zufällig gewählten Punkten . Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 2(1963), 75–84.CrossRefGoogle Scholar
Rényi, A. and Sulanke, R., Über die konvexe Hülle von $n$ zufällig gewählten Punkten. II . Z. Wahrscheinlichkeitstheorie und Verw Gebiete 3(1996), 138–147.CrossRefGoogle Scholar
Schneider, R., Intersection probabilities and kinematic formulas for polyhedral cones . Acta Math. Hungar. 155(2018), 3–24.CrossRefGoogle Scholar
Schneider, R., Conic support measures . J. Math. Anal. Appl. 471(2019), 812–825.CrossRefGoogle Scholar
Schneider, R. and Weil, W., Stochastic and integral geometry . Springer, New York, NY, 2008.CrossRefGoogle Scholar
Thäle, C., Turchi, N., and Wespi, F., Random polytopes: central limit theorems for intrinsic volumes . Proc. Am. Math. Soc. 146(2018), 3063–3071.CrossRefGoogle Scholar
Wendel, J. G., A problem in geometric probability . Math. Scand. 11(1096), 109–111.CrossRefGoogle Scholar