Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T19:23:30.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Nearly Approximate Transitivity (AT) for Circulant Matrices

Part of: Normed linear spaces and Banach spaces; Banach lattices Ordered structures Ergodic theory Measure-theoretic ergodic theory Stochastic processes

Published online by Cambridge University Press:  07 March 2019

David Handelman
David Handelman*
Affiliation:
Mathematics Department, University of Ottawa, Ottawa, ON K1N 6N5 Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By previous work of Giordano and the author, ergodic actions of 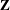$\mathbf{Z}$ (and other discrete groups) are completely classified measure-theoretically by their dimension space, a construction analogous to the dimension group used in 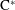$\text{C}^{\ast }$-algebras and topological dynamics. Here we investigate how far from approximately transitive (AT) actions can be that derive from circulant (and related) matrices. It turns out not very: although non-AT actions can arise from this method of construction, under very modest additional conditions, approximate transitivity arises. KIn addition, if we drop the positivity requirement in the isomorphism of dimension spaces, then all these ergodic actions satisfy an analogue of AT. Many examples are provided.

Keywords

approximately transitiveergodic transformationcirculant matrixhemicirculant matrixdimension spacematrix-valued random walk

MSC classification

Primary: 37A05: Measure-preserving transformations
Secondary: 06F25: Ordered rings, algebras, modules 28D05: Measure-preserving transformations 46B40: Ordered normed spaces 60G50: Sums of independent random variables; random walks
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 2 , April 2019 , pp. 381 - 415
Copyright
© Canadian Mathematical Society 2019 

Footnotes

Supported in part by an NSERC Discovery Grant.

References

Alfsen, E. M., Compact convex sets and boundary integrals. Ergebnisse der Mathematik und ihrer Grenzgebiete, 57. Springer–Verlag, New York, 1971.Google Scholar
Asimow, L. and Ellis, A. J., Convexity theory and its applications in functional analysis. London Mathematical Society Monographs, 16. Academic Press, New York, 1980.Google Scholar
Baker, B. M. and Handelman, D. E., Positive polynomials and time dependent integer-valued random variables . Canad J. Math. 44(1992), 3–41. https://doi.org/10.4153/CJM-1992-001-6.Google Scholar
Bezuglyi, S. and Handelman, D., Measures on Cantor sets: the good, the ugly, the bad . Trans. Amer. Math. Soc. 366(2014), 6247–6311. https://doi.org/10.1090/S0002-9947-2014-06035-2.Google Scholar
Connes, A. and Woods, E. J., Hyperfinite von Neumann algebras and Poisson boundaries of time-dependent random walks . Pacific J. Math. 137(1989), 225–243. https://doi.org/10.2140/pjm.1989.137.225.Google Scholar
Dooley, A. and Quas, A., Approximate transitivity for zero-entropy systems . Ergodic Theory Dynam. Systems 25(2005), 443–453. https://doi.org/10.1017/S0143385704000525.Google Scholar
Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite-dimensional algebras . J. Algebra 38(1976), 29–44. https://doi.org/10.1016/0021-8693(76)90242-8.Google Scholar
Elliott, G. A. and Giordano, T., Amenable actions of discrete groups . Ergodic Theory Dynam. Systems 13(1993), 289–318. https://doi.org/10.1017/S0143385700007379.Google Scholar
Giordano, T. and Handelman, D., Matrix-valued random walks and variations on property AT . Münster J. Math. 1(2008), 15–72.Google Scholar
Goodearl, K. R. and Handelman, D. E., Metric completions of partially ordered abelian groups . Indiana Univ Math. J. 29(1980), 861–895. https://doi.org/10.1512/iumj.1980.29.29060.Google Scholar
Handelman, D., Isomorphisms and non-isomorphisms of AT actions . J. Anal. Math. 108(2009), 293–366. https://doi.org/10.1007/s11854-009-0026-z.Google Scholar
Handelman, D. and Rossmann, W., Actions of compact groups on AF C*-algebras . Illinois J. Math. 29(1985), 51–95.Google Scholar
Munteanu, R. B., Entropy of AT(n) systems. arxiv:1412.2038.Google Scholar
Vershik, A. M., Uniform algebraic approximation of shift and multiplication operators . Dokl Akad Nauk SSSR 259(1981), 526–529.Google Scholar