Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Temam, Roger
2000.
Development of Mathematics, 1950–2000.
p.
1049.
Moschandreou, Terry Eleftherios
and
Afas, Keith Christian
2021.
Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics.
Applied Mechanics,
Vol. 2,
Issue. 3,
p.
613.


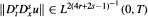 and max
and max 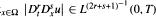 , up to any given integer value of the weighted order 2
, up to any given integer value of the weighted order 2