Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T04:26:39.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Murnaghan-Nakayama Rules for Characters of Iwahori-Hecke Algebras of the Complex Reflection Groups G(r, p, n)

Published online by Cambridge University Press:  20 November 2018

Tom Halverson  and
Arun Ram
Tom Halverson
Affiliation:
Department of Mathematics Macalester College St. Paul, MN USA
Arun Ram
Affiliation:
Department of Mathematics Princeton University Princeton, NJ 08544 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

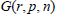Iwahori-Hecke algebras for the infinite series of complex reflection groups $G(r,\,p,\,n)$ were constructed recently in the work of Ariki and Koike [AK], Broué and Malle [BM], and Ariki [Ari]. In this paper we give Murnaghan-Nakayama type formulas for computing the irreducible characters of these algebras. Our method is a generalization of that in our earlier paper [HR] in which we derived Murnaghan-Nakayama rules for the characters of the Iwahori-Hecke algebras of the classical Weyl groups. In both papers we have been motivated by C. Greene [Gre], who gave a new derivation of the Murnaghan-Nakayama formula for irreducible symmetric group characters by summing diagonal matrix entries in Young's seminormal representations. We use the analogous representations of the Iwahori-Hecke algebra of 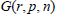$G(r,\,p,\,n)$ given by Ariki and Koike [AK] and Ariki [Ari].

Keywords

20C0505E05Markov-type inequalityBernstein-type inequalityNikolskii-type inequalitySchur-type inequalityrational functions with prescribed polescurved majorantsChebyshev polynomials
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 1 , 01 February 1998 , pp. 167 - 192
Copyright
Copyright © Canadian Mathematical Society 1998

References

[Ari] Ariki, S., Representation theory of a Hecke algebra of G(r, p. n). J. Algebra 177 (1995), 164–185.Google Scholar
[AK] Ariki, S. and Koike, K., A Hecke algebra of (ℤ/rℤ) ≀Sn and construction of its irreducible representations. Adv. Math. 106 (1994), 216–243.Google Scholar
[BM] Broué, M. and Malle, G., Zyklotomische Heckealgebren. Astérisque 212 (1993), 119–189.Google Scholar
[GP] Geck, M. and Pfeiffer, G.,On the irreducible characters of Hecke algebras. Adv. Math. 102 (1993), 79–94.Google Scholar
[Gre] Greene, C., A rational function identity related to the Murnaghan-Nakayama formula for the characters of Sn. J. Alg. Comb. 1 (1992), 235–255.Google Scholar
[HR] Halverson, T. and Ram, A., Murnaghan-Nakayama rules for the characters of Iwahori-Hecke algebras of classical type. Trans. Amer.Math. Soc. 348 (1996), 3967–3995.Google Scholar
[Hfs] Hoefsmit, P.N., Representations ofHecke algebras of finite groups with BN-pairs of classical type. Thesis, University of British Columbia, 1974.Google Scholar
[KW] King, R.C. and Wybourne, B.G., Representations and traces of Hecke algebras Hn(q. of type An-1. J. Math. Phys. 33 (1992), 4–14.Google Scholar
[Mac] Macdonald, I.G., Symmetric Functions and Hall Polynomials. Oxford University Press, 1979.Google Scholar
[Osi] Osima, M., On the representations of the generalized symmetric group .Math. J. Okayama Univ. 4 (1954), 39–56.Google Scholar
[Pfe1] Pfeiffer, G.,Character values of Iwahori-Hecke algebras of type B. In: Finite Reductive Groups: Related Structures and Representations (Ed. Cabanes, M.), Progress in Math. 141 (1996), 333–360.Google Scholar
[Pfe2] Pfeiffer, G. , Charakterwerte von Iwahori-Hecke-Algebren von klassischem Typ. Aachener Beiträge zur Mathematik 14 (1995), Verlag der Augustinus-Buchhandlung, Aachen.Google Scholar
[Ram] Ram, A., A Frobenius formula for the characters of the Hecke algebras. Invent. Math. 106 (1991), 461– 488.Google Scholar
[ST] Shephard, G.C. and Todd, J.A., Finite unitary reflection groups. Canad. J. Math. 6 (1954), 274–304.Google Scholar
[Sta] Stanley, R., Enumerative Combinatorics I. Wadsworth & Brooks/Cole, 1986.Google Scholar
[Ste] Stembridge, J., On the eigenvalues of representations of reflection groups and wreath products. Pacific J. Math. 140 (1989), 353–396.Google Scholar
[vdJ] van der Jeugt, J., An algorithm for characters of Hecke algebras Hn(q. of type An-1. J. Phys. A 24 (1991), 3719–3724.Google Scholar
[You] Young, A., Quantitative substitutional analysis I–IX. Proc. London Math. Soc. 1901–1952.Google Scholar