This paper studies conditions on an analytic function that imply it belongs to 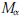${{M}_{\alpha }}$, the set of multipliers of the family of functions given by 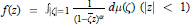$f(z)\,=\,{{\int }_{\left| \zeta \right|=1}}\,\frac{1}{{{(1-\overline{\zeta }z)}^{\alpha }}}d\mu (\zeta )\,(\left| z \right|\,<\,1)$ where 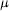$\mu $ is a complex Borel measure on the unit circle and 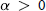$\alpha \,>\,0$. There are two main theorems. The first asserts that if 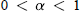$0\,<\,\alpha \,<\,1$ and 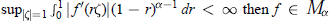${{\sup }_{\left| \zeta \right|=1}}\,\int_{0}^{1}{}\left| {f}'(r\zeta ) \right|{{(1-r)}^{\alpha -1}}\,dr<\infty \text{then}f\in {{M}_{\alpha }}$. The second asserts that if 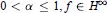$0\,<\,\alpha \,\le \,1,f\,\in \,{{H}^{\infty }}$ and 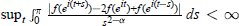$\sup {{}_{t\int_{0}^{\pi }{{}}}}\frac{\left| f({{e}^{i(t+s)}})-2f({{e}^{it}})+f({{e}^{i(t-s)}}) \right|}{{{s}^{2-\alpha }}}\,ds\,<\,\infty$ then 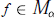$f\in {{M}_{\alpha }}$. The conditions in these theorems are shown to relate to a number of smoothness conditions on the unit circle for a function analytic in the open unit disk and continuous in its closure.