Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:29:29.246Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicative Integration of Infinite Products

Published online by Cambridge University Press:  20 November 2018

David Lowell Lovelady
David Lowell Lovelady*
Affiliation:
Georgia Institute of Technology, Atlanta, Georgia University of South Carolina, Columbia, South Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a complete normed abelian group with norm N1. Let S be an interval (bounded or otherwise) of real numbers. We propose to study the Stieltjes integral equation

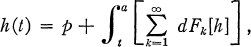
where p is in G, a is in S, and each Fk is a function on S each value of which is a function from G to G. Our primary tools of investigation will be the works of J. S. MacNerney [6; 7] and their extensions by the author [4; 5]. Our main result, Theorem 4, will show that the equation above can be solved by a product integral of infinite products of solutions for the summands of the integrator. After obtaining our results, we shall specialize them to a linear situation and then show how this specialization allows us to obtain representations for analytic functions having only invertible values in a complex Banach algebra with identity.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 692 - 698
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Gantmacher, F. R., The theory of matrices, Vol. II (Chelsea, New York, 1964).Google Scholar
2. Hille, E., Linear differential equations in Banach algebras, Proc. Int. Symp. on Linear Spaces, Jerusalem (1960), 263–273.Google Scholar
3. Hille, E., Lectures on ordinary differential equations (Addison-Wesley, Reading, Mass., 1969).Google Scholar
4. Lovelady, D. L., Perturbations of solutions of Stieltjes integral equations, Trans. Amer. Math. Soc. 155 (1971), 175–187.Google Scholar
5. Lovelady, D. L., Algebraic structure for a set of nonlinear integral operations (to appear in Pacific J. Math. 37 (1971)).Google Scholar
6. MacNerney, J. S., Integral equations and semigroups, Illinois J. Math. 7 (1963), 148–173.Google Scholar
7. Lovelady, D. L., A nonlinear integral operation, Illinois J. Math. 8 (1964), 621–638.Google Scholar
8. Rasch, G., Zur Théorie und Anwendung Produktintegrals, J. Reine Angew. Math. 171 (1934), 65–119.Google Scholar