Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-20T14:21:39.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicative Commutators of Operators

Published online by Cambridge University Press:  20 November 2018

Arlen Brown  and
Carl Pearcy
Arlen Brown
Affiliation:
University of Michigan
Carl Pearcy
Affiliation:
University of Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An invertible operator T on a Hilbert space 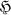is a multiplicative commutator if there exist invertible operators A and B on 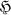such that T = ABA–1B–1. In this paper we discuss the question of which operators are, and which are not, multiplicative commutators. The analogous question for additive commutators (operators of the form AB — BA) has received considerable attention and has, in fact, been completely settled (2). The present results represent the information we have been able to obtain by carrying over to the multiplicative problem the techniques that proved efficacious in the additive situation. While these results remain incomplete, they suffice, for example, to enable us to determine precisely which normal operators are multiplicative commutators.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 737 - 749
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Brown, A., Halmos, P. R., and Pearcy, C., Commutators of operators on Hilbert space, Can. J. Math., 17 (1965), 695–708.Google Scholar
2. Brown, A. and Pearcy, C., Structure of commutators of operators, Ann. Math., 82 (1965), 112–127.Google Scholar
3. Deckard, D. and Pearcy, C., Another class of invertible operators without square roots, Proc. Amer. Math. Soc., 14(1963), 445–449.Google Scholar
4. Lumer, G. and Rosenblum, M., Linear operator equations, Proc. Amer. Math. Soc., 10 (1959), 32–41.Google Scholar
5. Pearcy, C., On commutators of operators on Hilbert space, Proc. Amer. Math. Soc, 16 (1965), 53–59.Google Scholar
6. Shoda, K., Über den Kommutator der Matrizen, J. Math. Soc. Japan, 3 (1951), 78–81.Google Scholar