No CrossRef data available.
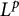 $L^p$-improving measures in
$L^p$-improving measures in 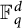 ${\Bbb F}_q^d$
${\Bbb F}_q^d$Published online by Cambridge University Press: 27 December 2023
The purpose of this paper is to introduce and study the following graph-theoretic paradigm. Let 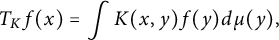 $$ \begin{align*}T_Kf(x)=\int K(x,y) f(y) d\mu(y),\end{align*} $$
$$ \begin{align*}T_Kf(x)=\int K(x,y) f(y) d\mu(y),\end{align*} $$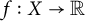 $f: X \to {\Bbb R}$, X a set, finite or infinite, and K and
$f: X \to {\Bbb R}$, X a set, finite or infinite, and K and 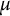 $\mu $ denote a suitable kernel and a measure, respectively. Given a connected ordered graph G on n vertices, consider the multi-linear form
$\mu $ denote a suitable kernel and a measure, respectively. Given a connected ordered graph G on n vertices, consider the multi-linear form 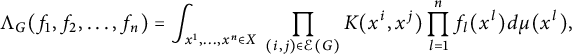 $$ \begin{align*}\Lambda_G(f_1,f_2, \dots, f_n)=\int_{x^1, \dots, x^n \in X} \ \prod_{(i,j) \in {\mathcal E}(G)} K(x^i,x^j) \prod_{l=1}^n f_l(x^l) d\mu(x^l),\end{align*} $$
$$ \begin{align*}\Lambda_G(f_1,f_2, \dots, f_n)=\int_{x^1, \dots, x^n \in X} \ \prod_{(i,j) \in {\mathcal E}(G)} K(x^i,x^j) \prod_{l=1}^n f_l(x^l) d\mu(x^l),\end{align*} $$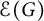 ${\mathcal E}(G)$ is the edge set of G. Define
${\mathcal E}(G)$ is the edge set of G. Define 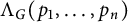 $\Lambda _G(p_1, \ldots , p_n)$ as the smallest constant
$\Lambda _G(p_1, \ldots , p_n)$ as the smallest constant 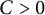 $C>0$ such that the inequality (0.1)
$C>0$ such that the inequality (0.1)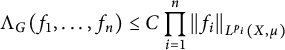 $$ \begin{align} \Lambda_G(f_1, \dots, f_n) \leq C \prod_{i=1}^n {||f_i||}_{L^{p_i}(X, \mu)} \end{align} $$
$$ \begin{align} \Lambda_G(f_1, \dots, f_n) \leq C \prod_{i=1}^n {||f_i||}_{L^{p_i}(X, \mu)} \end{align} $$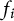 $f_i$,
$f_i$, 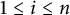 $1\le i\le n$, on X. The basic question is, how does the structure of G and the mapping properties of the operator
$1\le i\le n$, on X. The basic question is, how does the structure of G and the mapping properties of the operator 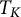 $T_K$ influence the sharp exponents in (0.1). In this paper, this question is investigated mainly in the case
$T_K$ influence the sharp exponents in (0.1). In this paper, this question is investigated mainly in the case 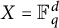 $X={\Bbb F}_q^d$, the d-dimensional vector space over the field with q elements,
$X={\Bbb F}_q^d$, the d-dimensional vector space over the field with q elements, 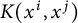 $K(x^i,x^j)$ is the indicator function of the sphere evaluated at
$K(x^i,x^j)$ is the indicator function of the sphere evaluated at 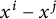 $x^i-x^j$, and connected graphs G with at most four vertices.
$x^i-x^j$, and connected graphs G with at most four vertices.
A. Iosevich and P. Bhowmik were supported in part by the National Science Foundation (Grant No. HDR TRIPODS-1934962) and the National Science Foundation (Grant No. DMS-2154232). D. Koh was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grant No. RS-2023-00249597). T. Pham was supported by the research project QG.23.03 of Vietnam National University, Hanoi.