Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T22:14:31.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Motivic Haar Measure on Reductive Groups

Published online by Cambridge University Press:  20 November 2018

Julia Gordon
Julia Gordon*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M4S 2E4 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define a motivic analogue of the Haar measure for groups of the form 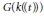$G(k((t)))$, where $k$ is an algebraically closed field of characteristic zero, and 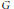$G$ is a reductive algebraic group defined over $k$. A classical Haar measure on such groups does not exist since they are not locally compact. We use the theory of motivic integration introduced by M. Kontsevich to define an additive function on a certain natural Boolean algebra of subsets of 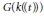$G(k((t)))$. This function takes values in the so-called dimensional completion of the Grothendieck ring of the category of varieties over the base field. It is invariant under translations by all elements of 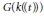$G(k((t)))$, and therefore we call it a motivic analogue of Haar measure. We give an explicit construction of the motivic Haar measure, and then prove that the result is independent of all the choices that are made in the process.

Keywords

14A1514L15motivic integrationreductive group
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 1 , 01 February 2006 , pp. 93 - 114
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Beauville, A. and Laszlo, Y., Conformal blocks and generalized theta functions. Comm. Math. Phys. 164(1994), 385–419.Google Scholar
[2] Bosch, S., Lütkebohmert, W., and Raynaud, M., Néron Models. Ergebnisse der Mathematik und ihrer Grenzgebiete 21, Springer-Verlag, Berlin, 1990.Google Scholar
[3] Carter, R. W., Simple Groups of Lie Type. John Wiley & Sons, NY 1972.Google Scholar
[4] Craw, A., An introduction to motivic integration, preprint http://xxx.lanl.gov/abs/math.AG/9911179. Google Scholar
[5] Denef, J. and Loeser, F., Motivic integration, quotient singularities and the McKay correspondence. Compositio Math 131(2002), 267–290.Google Scholar
[6] Eisenbud, D., Commutative algebra. With a view toward algebraic geometry. Graduate Texts in Mathematics 150, Springer-Verlag, New York, 1995.Google Scholar
[7] Greenberg, M., Schemata over local rings. Ann. of Math. 73(1961), 624–648.Google Scholar
[8] Hartshorne, R., Algebraic Geometry. Graduate Texts in Mathematics 52, Springer-Verlag, New York, 1977.Google Scholar
[9] Humphreys, J., Linear Algebraic Groups. Graduate Texts in Mathematics 21, Springer-Verlag, New York, 1975.Google Scholar
[10] Kashiwara, M., The flag manifold of Kac-Moody Lie algebra. In: Algebraic Analysis, Geometry, and Number Theory, Johns Hopkins Univ. Press, Baltimore, MD, 1989, pp. 161–190.Google Scholar
[11] Kontsevich, M., Lecture at Orsay, 1995.Google Scholar
[12] Loeser, F., Lecture at the workshop on Integration on arc spaces, elliptic genus and chiral DeRham complex. Banff, June 2003.Google Scholar
[13] Loeser, F. and Sebag, J., Motivic integration on smooth rigid varieties and invariants of degenerations. Duke Math. J. 119(2003), 315–344.Google Scholar
[14] Looijenga, E., Motivic Measures. Astérisque 276(2002), 267–297.Google Scholar
[15] Scholl, A., Classical motives, In: Motives: Proc. Sympos. Pure Math. 55, Part 1, American Mathematical Society, Providence, RI, 1994, pp. 163–187.Google Scholar