Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T06:46:26.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Monodromy Groups and Self-Invariance

Published online by Cambridge University Press:  20 November 2018

Isabel Hubard ,
Alen Orbanić  and
Asia Ivić Weiss
Isabel Hubard
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3 email: [email protected], [email protected]
Alen Orbanić
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 21, 1000 Ljubljana, Slovenia, EU email: [email protected]
Asia Ivić Weiss
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3 email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

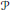For every polytope $\mathcal{P}$ there is the universal regular polytope of the same rank as 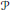$\mathcal{P}$ corresponding to the Coxeter group 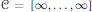$\mathcal{C}\,=\,\left[ \infty ,\,.\,.\,.\,,\,\infty \right]$. For a given automorphism $d$ of 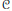$\mathcal{C}$, using monodromy groups, we construct a combinatorial structure 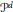${{P}^{d}}$. When 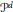${{P}^{d}}$ is a polytope isomorphic to 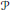$\mathcal{P}$ we say that 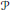$\mathcal{P}$ is self-invariant with respect to $d$, or $d$-invariant. We develop algebraic tools for investigating these operations on polytopes, and in particular give a criterion on the existence of a $d$-automorphism of a given order. As an application, we analyze properties of self-dual edge-transitive polyhedra and polyhedra with two flag-orbits. We investigate properties of medials of such polyhedra. Furthermore, we give an example of a self-dual equivelar polyhedron which contains no polarity (duality of order 2). We also extend the concept of Petrie dual to higher dimensions, and we show how it can be dealt with using self-invariance.

Keywords

51M2005C2505C1005C3052B70mapsabstract polytopesself-dualitymonodromy groupsmedials of polyhedra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1300 - 1324
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Ashley, J., Grünbaum, B., Shephard, G. C., and W., Stromquist, Self-duality groups and ranks of self-dualities. In: Applied Geometry and Discrete Mathematics. DI MACS Ser. Discrete Math. Theoret. Comput. Sci. 4, American Mathematical Society, Providence, RI, 1991, pp. 11–50.Google Scholar
[2] Breda D’Azevedo, A. and Nedela, R., Join and intersection of hypermaps. Acta Univ. M. Belii Ser. Math. 9(2001), 13–28.Google Scholar
[3] Brehm, U. and Schulte, E., Polyhedral maps. In: Handbook of Discrete and Computational Geometry. CRC Press Ser. Discrete Math. Appl., Boca Raton, FL, 1997, pp. 345–358.Google Scholar
[4] Bosma, W., Cannon, C., Playoust, C., The Magma algebra system. I. The user language. J. Symbolic Comput. 24(1997), no. 3-4, 235–265.Google Scholar
[5] Coxeter, H. S. M., Regular Polytopes., Third edition. Dover, New York, 1973.Google Scholar
[6] Graver, J. E. and Watkins, M. E., Locally Finite, Planar, Edge-Transitive Graphs. Mem. Amer. Math. Soc. 126(1997) 1997, no. 601.Google Scholar
[7] Grünbaum, B. and Shephard, G. C., Is self-duality always involutory? Amer. Math. Monthly 95(1988), no. 8, 729–733.Google Scholar
[8] Hartley, M. I., All polytopes are quotients and isomorphic polytopes are quotients by conjugate subgroups. Discrete Comput. Geom. 21(1999), no. 2, 289–298.Google Scholar
[9] Hartley, M. I., More on quotient polytopes. Aequationes Math. 57(1999), no. 1, 108–120.Google Scholar
[10] Hubard, I. and Ivić Weiss, A., Self-duality of chiral polytopes. J. Combin. Theory Ser. A 111(2005), no. 1, 128–136.Google Scholar
[11] James, L. D., Complexes and Coxeter groups—operations and outer automorphisms. J. Algebra 113(1988), no. 2, 339–345.Google Scholar
[12] Jendrol, S., A non-involutory selfduality. Discrete Math. 74(1989), no. 3, 325–326.Google Scholar
[13] Jones, G. A. and Thornton, J. S., Operations on maps, and outer automorphisms. J. Combin. Theory Ser. B 35(1983), no. 2, 93–103.Google Scholar
[14] Lins, S., Graph-encoded maps. J. Combin. Theory Ser. B 32(1982), no. 2, 171–181.Google Scholar
[15] Mc Mullen, P. and Schulte, E., Quotients of polytopes and C-groups. Discrete Comput. Geom. 11(1994), no. 4, 453–464.Google Scholar
[16] Mc Mullen, P. and Schulte, E., Abstract Regular Polytopes. In: Encyclopedia of Mathematics and its Applications 92, Cambridge University Press, Cambridge, 2002.Google Scholar
[17] Negami, S., Uniqueness and faithfullness of embedding of toroidal graphs. Discrete Math. 44(1983), no. 2, 161–180.Google Scholar
[18] Orbanić, A., Edge-transitive maps, Doctoral Dissertation, Univ. of Ljubljana, Ljubljana, 2006.Google Scholar
[19] Orbanić, A., F-actions and parallel-product decomposition of reflexible maps. J. Algebraic Combin. 26(2007), no. 4, 507–527.Google Scholar
[20] Richter, R. B., Širáň, J., Jajcay, R., Tucker, T. W., and Watkins, M. E., Cayley maps. J. Combin. Theory Ser. B 95(2005), no. 2, 189–245.Google Scholar
[21] Schulte, E. and Weiss, A. I., Problems on polytopes, their groups, and realizations. Period. Math. Hungar. 53(2006), no. 1-2, 231–255.Google Scholar
[22] Širáň, J., Tucker, T. W., Watkins, M. E., Realizing finite edge-transitive orientable maps. J. Graph Theory 37(2001), no. 1, 1–34.Google Scholar
[23] Vince, A., Combinatorial maps. J. Combin. Theory Ser. B 34(1983), no. 1, 1–21.Google Scholar
[24] Wilson, S. E., Operators over regular maps. Pacific J. of Math. 81(1979), no. 2, 559–568.Google Scholar
[25] Wilson, S. E., Parallel products in groups and maps. J. Algebra 167(1994), no. 3, 539–546.Google Scholar
[26] Wilson, S. E.,Wilson's census of rotary maps. http://www.ijp.si/Regular Maps/.Google Scholar