Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T00:03:55.070Z Has data issue: false hasContentIssue false
  • English
  • Français

Monodromy Filtrations and the Topology of Tropical Varieties

Published online by Cambridge University Press:  20 November 2018

David Helm  and
Eric Katz
David Helm
Affiliation:
Department of Mathematics, University of Texas at Austin, 1 University Station C1200, Austin, TX 78712- 0257, USA email: [email protected]
Eric Katz
Affiliation:
Department of Mathematics, University of Texas at Austin, 1 University Station C1200, Austin, TX 78712- 0257, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

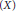We study the topology of tropical varieties that arise from a certain natural class of varieties. We use the theory of tropical degenerations to construct a natural, “multiplicity-free” parameterization of Trop$\left( X \right)$ by a topological space 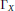${{\Gamma }_{X}}$ and give a geometric interpretation of the cohomology of 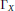${{\Gamma }_{X}}$ in terms of the action of a monodromy operator on the cohomology of $X$. This gives bounds on the Betti numbers of 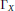${{\Gamma }_{X}}$ in terms of the Betti numbers of $X$ which constrain the topology of Trop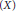$\left( X \right)$. We also obtain a description of the top power of the monodromy operator acting on middle cohomology of $X$ in terms of the volume pairing on 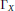${{\Gamma }_{X}}$.

Keywords

14T0514D06
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 845 - 868
Copyright
Copyright © Canadian Mathematical Society 2012

References

[B1] Berkovich, V., Smooth p-adic analytic spaces are locally contractible. Invent. Math. 137(1999), 1–84. http://dx.doi.org/10.1007/s002220050323 Google Scholar
[B2] Berkovich, V., An analog of Tate's conjecture over local and finitely generated fields. Internat. Math. Res. Notices 2000, 665–680.Google Scholar
[BGS] Burgos Gil, J. and M. Sombra. When do the recession cones of a polyhedral complex form a fan? Preprint, arxiv:1008.2608.Google Scholar
[d J] de Jong, A. J., Smoothness, semistability, and alterations. Inst. Hautes Études Sci. Publ. Math. 83(1996), 51–93.Google Scholar
[D1] Deligne, P., Théorie de Hodge I. In: Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, Gauthier-Villars, Paris, 1971, 425–430.Google Scholar
[D2] Deligne, P., La conjecture de Weil II. Inst. Hautes Études Sci. Publ. Math. 52(1980), 137–252.Google Scholar
[EKL] Einsiedler, M., Kapranov, M., and Lind, D., Non-Archimedean amoebas and tropical varieties. J. Reine Angew. Math. 601(2006), 139–157. http://dx.doi.org/10.1515/CRELLE.2006.097 Google Scholar
[F] Fulton, W., Introduction to Toric Varieties. Princeton University Press, 1993.Google Scholar
[GS] Gross, M. and Siebert, B., Mirror Symmetry via Logarithmic Degeneration Data II. Preprint, arxiv:0709.2290. http://dx.doi.org/10.1090/S1056-3911-2010-00555-3 Google Scholar
[SGA 7I] Grothendieck, A., Modèles de Néron et monodromie. SGA 7 I, Exposé IX, Lecture Notes in Math. 288, Springer-Verlag, New York, 1972, 313–523.Google Scholar
[H] Hacking, P., The homology of tropical varieties. Collect. Math. 59(2008), 263–273. http://dx.doi.org/10.1007/BF03191187 Google Scholar
[HKT] Hacking, P., Keel, S. and Tevelev, J., Stable pair, tropical, and log canonical compact moduli of del Pezzo surfaces. Invent. Math. 178(2009), 173–227. http://dx.doi.org/10.1007/s00222-009-0199-1 Google Scholar
[I] Ito, T., Weight-monodromy conjecture over equal characteristic local fields. Amer. J. Math. 127(2005), 647–658. http://dx.doi.org/10.1353/ajm.2005.0022 Google Scholar
[KKMS] Kempf, G., Knudsen, F., Mumford, D. and B. Saint-Donat, Toroidal embeddings. I. Lecture Notes in Mathematics 339, Springer-Verlag, Berlin-New York, 1973.Google Scholar
[KMM] Katz, E., Markwig, H. and Markwig, T., The tropical j-invariant. LMS J. Comput. Math. 12(2009), 275–294.Google Scholar
[KS10] Katz, E. and Stapledon, A., The tropical motivic nearby fiber. Preprint, arxiv:1007.0411.Google Scholar
[KS06] Kontsevich, M. and Soibelman, Y., Affine structures and non-Archimedean analytic spaces. In: The unity of mathematics, Birkhäuser Boston, Boston, MA, 2006, 321–385.Google Scholar
[LQ] Luxton, M. and Qu, Z., On Tropical Compactification. Preprint, arxiv:0902.2009.Google Scholar
[MZ] Mikhalkin, G. and Zharkov, I., Tropical curves, their Jacobians, and theta functions. In: Curves and abelian varieties, Contemp. Math. 465, Amer. Math. Soc., Providence, RI, 2008, 203–230.Google Scholar
[NS] Nishinou, T. and Siebert, B., Toric degenerations of toric varieties and tropical curves. Duke Math. J. 135(2006), 1–51. http://dx.doi.org/10.1215/S0012-7094-06-13511-1 Google Scholar
[P] Payne, S., Analytification is the limit of all tropicalizations.Math. Res. Lett. 16(2009), 543–556.Google Scholar
[RZ] Rapoport, M. and Zink, T., Über die lokale Zetafunktion von Shimuravarietäten, Monodromiefiltrations und verschwindende Zyklen in ungleicher Characteristik. Invent. Math. 68(1980), 21–101. http://dx.doi.org/10.1007/BF01394268 Google Scholar
[Si] Silverman, J., Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Mathematics 241, Springer-Verlag, New York, 1994.Google Scholar
[S] Smirnov, A. L., Torus schemes over a discrete valuation ring. Algebra i Analiz 8(1996), 161–172; translation in St. Petersburg Math. J. 8(1997), 651–659.Google Scholar
[Sch] Schneider, P., Basic notions of rigid analytic geometry. In: Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996), London Math. Soc. Lecture Note Ser. 254, Cambridge University Press, 1998, 369–379.Google Scholar
[Sp1] Speyer, D., Tropical Geometry. Ph D thesis, UC Berkeley, 2005.Google Scholar
[Sp2] Speyer, D., Uniformizing tropical curves I: genus zero and one. Preprint, arxiv:0711.2677.Google Scholar
[T] Tevelev, J., Compactifications of subvarieties of tori. Amer. J. Math. 129(2007), 1087–1104. http://dx.doi.org/10.1353/ajm.2007.0029Google Scholar