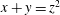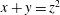Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sanders, Tom
2020.
Bootstrapping partition regularity of linear systems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 3,
p.
630.
Schoen, Tomasz
2021.
A Diophantine Ramsey Theorem.
Combinatorica,
Vol. 41,
Issue. 4,
p.
581.
Fernández-Bretón, David J.
2022.
Using Ultrafilters to Prove Ramsey-type Theorems.
The American Mathematical Monthly,
Vol. 129,
Issue. 2,
p.
116.
Chapman, Jonathan
2022.
Partition Regularity for Systems of Diagonal Equations.
International Mathematics Research Notices,
Vol. 2022,
Issue. 17,
p.
13272.
Liu, Hong
Pach, Péter Pál
and
Sándor, Csaba
2022.
Polynomial Schur’s Theorem.
Combinatorica,
Vol. 42,
Issue. S2,
p.
1357.
Baja, Zsolt
Dobák, Dániel
Kovács, Benedek
Pach, Péter Pál
and
Pigler, Donát
2023.
Towards characterizing the 2-Ramsey equations of the form ax + by = p(z).
Discrete Mathematics,
Vol. 346,
Issue. 5,
p.
113324.
Frantzikinakis, Nikos
Klurman, Oleksiy
and
Moreira, Joel
2025.
Partition regularity of Pythagorean pairs.
Forum of Mathematics, Pi,
Vol. 13,
Issue. ,