No CrossRef data available.
Article contents
Modular and Admissible Semilattices
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We correct some errors in [1] and extend some of the results there. Generally, we shall follow the terminology and notation of [1]. There is an error in the proof of Lemma 3.13 there, and consequently the subsequent results which depend on it are incorrect as stated. However, they are correct if we replace the condition “a-admissible” by “strongly a-admissible” (see [3] where this notion was introduced). We also show that the results in [1] are correct if the semilattices are assumed to be modular.
We shall change the terminology in [3] slightly.
Definition 1 (see [3]). Let A be a Boolean algebra and let D be a meet semilattice with 1. An admissible map f.A X D → D is called strongly admissible if
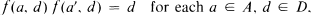
where a’ is the complement of a in A.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1984
References
1.
Hoo, C. S., Pseudocomplemented and implicative semilattices,
Can. J. Math.
35 (1982), 423–437.Google Scholar
2.
Murtv, P V. Ramana, Prime and implicative semilattices.
Algebra Universalis
10 (1980), 31–35.Google Scholar
3.
Murty, P. V. Ramana and Rao, V. V. Rama, Characterization of certain classes of pseudocomplemented semilattices.
Algebra Universalis
4 (1974), 289–300.Google Scholar
4.
Murty, P. V. Ramana and Murty, M. Krishna, On admissible semilattices,
Algebra Universalis
6 (1976), 355–366.Google Scholar
You have
Access