Article contents
Minimal Transitive Factorizations of Permutations into Cycles
Published online by Cambridge University Press: 20 November 2018
Abstract
We introduce a new approach to an enumerative problem closely linked with the geometry of branched coverings, that is, we study the number 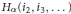 ${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ of ways a given permutation (with cycles described by the partition
${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ of ways a given permutation (with cycles described by the partition  $\alpha $) can be decomposed into a product of exactly
$\alpha $) can be decomposed into a product of exactly 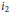 ${{i}_{2}}$ 2-cycles,
${{i}_{2}}$ 2-cycles, 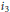 ${{i}_{3}}$ 3-cycles, etc., with certain minimality and transitivity conditions imposed on the factors. The method is to encode such factorizations as planar maps with certain descent structure and apply a new combinatorial decomposition to make their enumeration more manageable. We apply our technique to determine
${{i}_{3}}$ 3-cycles, etc., with certain minimality and transitivity conditions imposed on the factors. The method is to encode such factorizations as planar maps with certain descent structure and apply a new combinatorial decomposition to make their enumeration more manageable. We apply our technique to determine 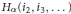 ${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ when
${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ when  $\alpha $ has one or two parts, extending earlier work of Goulden and Jackson. We also show how these methods are readily modified to count inequivalent factorizations, where equivalence is defined by permitting commutations of adjacent disjoint factors. Our technique permits us to generalize recent work of Goulden, Jackson, and Latour, while allowing for a considerable simplification of their analysis.
$\alpha $ has one or two parts, extending earlier work of Goulden and Jackson. We also show how these methods are readily modified to count inequivalent factorizations, where equivalence is defined by permitting commutations of adjacent disjoint factors. Our technique permits us to generalize recent work of Goulden, Jackson, and Latour, while allowing for a considerable simplification of their analysis.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
- 4
- Cited by


