Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:08:33.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal Plat Representations of Prime Knots and Links are not Unique

Published online by Cambridge University Press:  20 November 2018

José M. Montesinos
José M. Montesinos*
Affiliation:
Universidad Complutense, Madrid-3, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

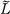Let denote the 2-fold cyclic covering space branched over a link L in S3. We wish to describe an infinite family of prime knots and links in which each member L exhibits two minimal 6-plat representations, where the associated Heegaard splittings of 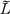are minimal and inequivalent. Thus each knot or link of that family admits at least two equivalence classes of 6-plat representations which are minimal.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 161 - 167
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Birman, J. S. and Hilden, H. M., On the mapping class group of closed, orientable surfaces as covering spaces, Annals of Math. Studies 66, 81–115.Google Scholar
2. Birman, J. S., On the equivalence of Heegaard splittings of closed, orientable 3-manifolds, Knots, Groups and 3-Manifolds (L. Neuwirth, Editor), Annals of Math. Studies 84 (1975), 137–164.Google Scholar
3. Birman, J. S., F. Gonzalez-Acufïa and Montesinos, J. M., Heegaard splittings of prime 3-manifolds are not unique, to appear, Michigan Math. J.Google Scholar
4. Birman, J. S., Braids, links and mapping class groups, Annals of Math. Studies 82 (1975).Google Scholar
5. Birman, J. S., On the stable equivalence of plat representations of knots and links, to appear, Can. J. Math.Google Scholar
6. Engmann, R., Nicht-hom'ôomorphe Heegaard-Zerlegungen vom Geschlecht 2 der zusammenhdngendem Summe zweier Linsenrâume, Abh. Math. Sem. Univ. Hamburg 35 (1970), 33–38.Google Scholar
7. Montesinos, J. M., Sobre la conjetura de Poincaré y los recubridores ramificados sobre un nudo, Tesis doctoral, Madrid, 1971.Google Scholar
8. Montesinos, J. M., Variedades de Seifert que son recubridores ciclicos ramificados de dos hojas, Boletin Soc. Mat. Mexicana 18 (1973), 1–32.Google Scholar
9. Reidemeister, K., Zur dreidimensionalen Topologie, Abh. Math. Sem. Univ. Hamburg 9 (1933), 189–194.Google Scholar
10. Seifert, H., Topologie dreidimensionaler gefaserter Raume, Acta Math. 60 (1933), 147–238.Google Scholar
11. Singer, J., Three dimensional manifolds and their Heegaard diagrams, Trans. Amer. Math. Soc. 85 (1933), 88–111.Google Scholar
12. Viro, O. Ja., Linkings, 2-sheeted branched coverings, and braids, Math. U.S.S.R. Sbornik 16 (1972), 222–236 (English translation).Google Scholar
13. Waldhausen, F., Eine Klasse von 3-dimensionalen Mannigfaltigkeiten II, Invent. Math 4 (1967), 87–117.Google Scholar
14. Waldhausen, F., Uber Involutionen der 3-Sphare, Topology 8 (1969), 81–91.Google Scholar