Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T00:03:53.476Z Has data issue: false hasContentIssue false
  • English
  • Français

The Minimal Growth Rate of Cocompact Coxeter Groups in Hyperbolic 3-space

Published online by Cambridge University Press:  20 November 2018

Ruth Kellerhals  and
Alexander Kolpakov
Ruth Kellerhals
Affiliation:
Department of Mathematics, University of Fribourg, Fribourg Pérolles, Switzerland. e-mail: [email protected]@unifr.ch
Alexander Kolpakov
Affiliation:
Department of Mathematics, University of Fribourg, Fribourg Pérolles, Switzerland. e-mail: [email protected]@unifr.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Due to work of 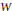$\text{W}$. Parry it is known that the growth rate of a hyperbolic Coxeter group acting cocompactly on 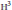${{\mathbb{H}}^{3}}$ is a Salem number. This being the arithmetic situation, we prove that the simplex group (3,5,3) has the smallest growth rate among all cocompact hyperbolic Coxeter groups, and that it is, as such, unique. Our approach provides a different proof for the analog situation in 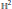${{\text{H}}^{2}}$ where $\text{E}$. Hironaka identified Lehmer's number as the minimal growth rate among all cocompact planar hyperbolic Coxeter groups and showed that it is (uniquely) achieved by the Coxeter triangle group (3,7).

Keywords

20F5522E4051F15Hyperbolic Coxeter groupgrowth rateSalem number
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 354 - 372
Copyright
Copyright © Canadian Mathematical Society 2014

References

[CaW] Cannon, J.W. and Wagreich, P., Growth functions of surface groups. Math. Ann. 293(1992), no. 2, 239–257. http://dx.doi.org/10.1007/BF01444714 Google Scholar
[CD] Charney, R. and Davis, M., Reciprocity of growth functions of Coxeter groups. Geom. Dedicata 39(1991), no. 3, 373–378.Google Scholar
[ChFr] Chinburg, T. and Friedman, E., The smallest arithmetic hyperbolic three-orbifold. Invent. Math. 86(1986), no. 3, 507–527. http://dx.doi.org/10.1007/BF01389265 Google Scholar
[Co] Coxeter, H. S. M., Discrete groups generated by reflections. Ann. Math. 35(1934), no. 3, 588–621. http://dx.doi.org/10.2307/1968753 Google Scholar
[CoMo] Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups. Fourth ed., Ergebnisse derMathematik und ihrer Grenzgebiete, 14, Springer-Verlag, Berlin-New York, 1980.Google Scholar
[D] Davis, M.W., The geometry and topology of Coxeter groups. London Mathematical Society Monographs, 32, Princeton University Press, Princeton, NJ, 2008.Google Scholar
[FlPl] Floyd, W. J. and Plotnick, S. P., Symmetries of planar growth functions. Invent. Math 93(1988), no. 3, 501–543. http://dx.doi.org/10.1007/BF01410198 Google Scholar
[GM] Gehring, F.W. and Martin, G. J., Minimal co-volume hyperbolic lattices. I. The spherical points of a Kleinian group. Ann. of Math. 170(2009), no. 1, 123–161. http://dx.doi.org/10.4007/annals.2009.170.123 Google Scholar
[GhHi] E., Ghate and Hironaka, E., The arithmetic and geometry of Salem numbers. Bull. Amer. Math. Soc. 38(2001), no. 3, 293–314. http://dx.doi.org/10.1090/S0273-0979-01-00902-8 Google Scholar
[He] Heckman, G. J., The volume of hyperbolic Coxeter polytopes of even dimension. Indag. Math. (N.S.) 6(1995), no. 2, 189–196. http://dx.doi.org/10.1016/0019-3577(95)91242-N Google Scholar
[Hi] Hironaka, E., The Lehmer polynomial and pretzel links. Canad. Math. Bull. 44(2001), no. 4, 440–451. http://dx.doi.org/10.4153/CMB-2001-044-x Google Scholar
[Im] Im Hof, H.-C., Napier cycles and hyperbolic Coxeter groups. Bull. Soc. Math. Belg. Sér. A 42(1990), no. 3, 523–545.Google Scholar
[In] Inoue, T., Organizing volumes of right-angled hyperbolic polyhedra. Algebr. Geom. Topol. 8(2008), no. 3, 1523–1565. http://dx.doi.org/10.2140/agt.2008.8.1523 Google Scholar
[Ka] Kaplinskaja, I. M., The discrete groups that are generated by reflections in the faces of simplicial prisms in Lobachevsii spaces. Math. Notes 15(1974), 88–91.Google Scholar
[Ke] Kellerhals, R., On the volume of hyperbolic polyhedra. Math. Ann. 285(1989), no. 4, 541–569. http://dx.doi.org/10.1007/BF01452047 Google Scholar
[MaM] T. H. Marshall, and Martin, G. J., Minimal co-volume hyperbolic lattices. II: Simple torsion in a Kleinian group. Ann. of Math. 176(2012), no. 1, 261–301. http://dx.doi.org/10.4007/annals.2012.176.1.4 Google Scholar
[Mi] Milnor, J., A note on curvature and fundamental group. J. Differential Geometry 2(1968), 1–7.Google Scholar
[Pa] Parry, W., Growth series of Coxeter groups and Salem numbers. J. Algebra 154(1993), no. 2, 406–415. http://dx.doi.org/10.1006/jabr.1993.1022 Google Scholar
[Pr] Prasolov, V. V., Polynomials. Algorithms and Computation in Mathematics, 11, Springer-Verlag, Berlin, 2004.Google Scholar
[R] Rotman, J., Galois theory. Universitext, Springer-Verlag, New York, 1998.Google Scholar
[Si] Siegel, C. L., Some remarks on discontinuous groups. Ann. of Math. 46(1945), 708–718. http://dx.doi.org/10.2307/1969206 Google Scholar
[So] Solomon, L., The orders of the finite Chevalley groups. J. Algebra 3(1966), 376–393. http://dx.doi.org/10.1016/0021-8693(66)90007-X Google Scholar
[St] Steinberg, R., Endomorphisms of linear algebraic groups. Memoirs of the American Mathematical Society, 80, American Mathematical Society, Providence, RI, 1968.Google Scholar
[Ve] Vesnin, A. Yu., Volumes of hyperbolic Löbell 3-manifolds. Math. Notes 64(1998), no. 1–2, 15–19.Google Scholar
[Vi1] Vinberg, È. B. and Shvartsman, O. V., Discrete groups of motions of spaces of constant curvature. In: Geometry, II, Encyclopaedia Math. Sci., 29, Springer, Berlin, 1993.Google Scholar
[Vi2] Vinberg, È. B., Hyperbolic reflection groups. Russian Math. Surveys 40(1985), 31–75.Google Scholar
[W] Worthington, R. L., The growth series of compact hyperbolic Coxeter groups with 4 and 5 generators. Canad. Math. Bull. 41(1998), 231–239. http://dx.doi.org/10.4153/CMB-1998-033-5 Google Scholar