Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T23:58:32.787Z Has data issue: false hasContentIssue false
  • English
  • Français

The Minimal Free Resolution of Fat Almost Complete Intersections in ℙ1 × ℙ1

Published online by Cambridge University Press:  20 November 2018

Giuseppe Favacchio  and
Elena Guardo
Giuseppe Favacchio
Affiliation:
Dipartimento di Matematica e Informatica, Viale A. Doria, 6 - 95100 - Catania, Italy e-mail: [email protected], [email protected]
Elena Guardo
Affiliation:
Dipartimento di Matematica e Informatica, Viale A. Doria, 6 - 95100 - Catania, Italy e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A current research theme is to compare symbolic powers of an ideal $I$ with the regular powers of $I$. In this paper, we focus on the case where 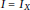$I\,=\,{{I}_{X}}$ is an ideal defining an almost complete intersection (ACI) set of points 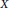$X$ in 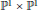${{\mathbb{P}}^{1}}\,\times \,{{\mathbb{P}}^{1}}$. In particular, we describe a minimal free bigraded resolution of a non-arithmetically Cohen-Macaulay (also non-homogeneous) set 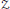$Z$ of fat points whose support is an ACI, generalizing an earlier result of Cooper et al. for homogeneous sets of triple points. We call 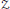$Z$ a fat ACI. We also show that its symbolic and ordinary powers are equal, i.e, 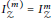$I_{Z}^{\left( m \right)}\,=\,I_{Z}^{m}$ for any 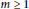$m\,\ge \,1$.

Keywords

13C4013F2013A1514C2014M05points in ℙ1 × ℙ1symbolic powersresolutionarithmetically Cohen-Macaulay
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 6 , 01 December 2017 , pp. 1274 - 1291
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bocci, C., Cooper, S., and Harbourne, B., Containment results for ideals of various configurations of points in . J. Pure Appl. Algebra 218(2014), 65–75. http://dx.doi.Org/10.1016/j.jpaa.2O13.04.012 Google Scholar
[2] Bocci, C. and Harbourne, B., Comparing powers and symbolic power of ideals. J. Algebraic Geometry 19(2010), 399–417.http://dx.doi.Org/10.1090/S1056-3911-09-00530-X Google Scholar
[3] Bocci, C., The resurgence of ideals of points and the containment problem. Proc. Amer. Math. Soc. 138(2010), 1175–1190.http://dx.doi.org/10.1090/S0002-9939-09-10108-9 Google Scholar
[4] CoCoATeam, , C0C0A: a system for doing Computations in Commutative Algebra. http://cocoa.dima.unige.it Google Scholar
[5] Cooper, S., Fatabbi, G., Guardo, E., Harbourne, B., Lorenzini, A., Migliore, J., Nagel, U., Seceleanu, A., Szpond, J., and Van Tuyl, A., Symbolic powers of codimension two Cohen-Macaulay ideals. arxiv:1606.00935 Google Scholar
[6] Grayson, D. R. and Stillman, M. E., Macaulay 2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/. Google Scholar
[7] Guardo, E., Harbourne, B., and Van Tuyl, A., Asymptotic resurgences for ideals of positive dimensional subschemes of projective space. Adv. Math. 246(2013), 114–127.http://dx.doi.Org/10.1016/j.aim.2013.05.027 Google Scholar
[8] Guardo, E., Fat lines in F3: regular versus symbolic powers. J. Algebra 390(2013), 221–230.http://dx.doi.Org/10.1016/j.jalgebra.2013.05.028 Google Scholar
[9] Guardo, E., Symbolic powers versus regular powers of ideals of general points in p1 × p1. Canad. J. Math. 65(2013), 823–842.http://dx.doi.Org/10.4153/CJM-2O12-045-3 Google Scholar
[10] Guardo, E. and Van Tuyl, A., Arithmetically Cohen-Macaulay sets of points in . Springer Briefs in Mathematics, Springer, Cham, 2015.Google Scholar
[11] Guardo, E., Fat points in and their Hilbert functions. Canad. J. Math. 56(2004), 716–741.http://dx.doi.Org/10.4153/CJM-2004-033-0 Google Scholar
[12] Hochster, M. and Huneke, C., Comparison of symbolic and ordinary powers of ideals. Invent. Math. 147(2002), 349–369.http://dx.doi.Org/10.1007/s00222O100176 Google Scholar
[13] Zariski, O. and Samuel, P., Commutative algebra. Vol. II. The University Series in Higher Mathematics, D. Van Nostrand Co., Inc., Princeton, N. J.-Toront-London-New York, 1960.Google Scholar