Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:32:01.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Metrizability of Finite Dimensional Spaces with a Binary Convexity

Published online by Cambridge University Press:  20 November 2018

M. Van de Vel
M. Van de Vel*
Affiliation:
Vrije Universiteit Amsterdam, Amsterdam, The Netherlands
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A convex structure consists of a set X, together with a collection 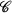of subsets of X, which is closed under intersection and under updirected union. The members of 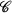are called convex sets, and 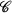is a convexity on X. Fox A a subset of X, h (A) denotes the (convex) hull of A. If A is finite, then h(A) is called a polytope, 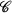is called a binary convexity if each finite collection of pairwise intersecting convex sets has a nonempty intersection. See [8], [21] for general references.

If X is also equipped with a topology, then the corresponding weak topology is the one generated by the convex closed sets. It is usually assumed that at least all polytopes are closed. 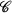is called normal provided that for each two disjoint convex closed sets C, D there exist convex closed sets C′, D′, with

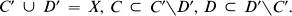
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 1 , 01 February 1986 , pp. 1 - 18
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Déak, E., Theory and applications of directional structures, Coll. Math. Soc. Jaos Bolyai 8, Topics in Topology, Keszthely (1972), 187–211.Google Scholar
2. Dilworth, R. P., A decomposition theorem for partially ordered sets, Ann. Math. 51 (1950), 161–166.Google Scholar
3. Engelking, R., General topology (PWN – Polish Scientific Publishers, Warszawa, 1977).Google Scholar
4. Eberhart, C., Metrizability of trees, Fund. Math. 65 (1969), 43–50.Google Scholar
5. Erdös, P., Graph theory and probability, Can. J. Math. 77 (1959), 34–38.Google Scholar
6. Gierz, G. et al, A compendium of continuous lattices (Springer Verlag, Berlin, 1980).CrossRefGoogle Scholar
7. de Groot, J., Super compactness and superextensions, Contributions to extension theory of topological structures, Symp. Berlin 1967, Deutsche Verslag der Wissensch. (Berlin, 1969), 89–90.Google Scholar
8. Jamison, R. E., A general theory of convexity, Dissertation, University of Washington, Seattle (1974).Google Scholar
9. Jamison, R. E., Partition numbers for trees and ordered sets, Pacific J. Math. 96 (1981), 115–140.Google Scholar
10. van Mill, J., Superextensions and Wallman spaces, MC tract 85 (Amsterdam, 1977).Google Scholar
11. van Mill, J., Superextensions of metrizable continua are Hilbert cubes, Fund. Math. 107 (1980), 201–224.Google Scholar
12. van Mill, J. and Schrijver, A., Subbase characterizations of compact spaces, Gen. Top. Appl. 70 (1979), 183–201.Google Scholar
13. van Mill, J. and van de Vel, M., Path connectedness, contractibility, and LC properties of superextensions, Bull. Acad. Pol. Sci. 26 (1978), 261–269.Google Scholar
14. van Mill, J. and van de Vel, M., Convexity preserving mappings in subbase convexity theory, Proc. Kon. Ned. Akad. Wet. A 81 (1978), 76–90.Google Scholar
15. van Mill, J. and van de Vel, M., Equality of the Lebesgue and the inductive dimension functions for compact spaces with a uniform convexity, Coll. Math. 50 (1985), 43–56.Google Scholar
16. van Mill, J. and Wattel, E., An external characterization of spaces which admit binary normal subbases, Amer. J. Math. 100 (1978), 987–994.Google Scholar
17. van Mill, J. and Wattel, E., Subbase characterizations of subspaces of compact trees, Top. Appl. 13 (1982), 321–326.Google Scholar
18. Sierksma, G., Axiomatic convexity theory and the convex product space, Dissertation, University of Groningen (Netherlands, 1976).Google Scholar
19. Stralka, A. R., Locally convex topological lattices, Trans. Amer. Math. Soc. 151 (1970), 629–640.Google Scholar
20. van de Vel, M., Superextensions and Lefschetz fixed point structures, Fund. Math. 104 (1979), 33–48.Google Scholar
21. van de Vel, M., Pseudo-boundaries and pseudo-interiors for topological convexities, Dissert. Math. 270 (1983), 1–72.Google Scholar
22. van de Vel, M., Finite dimensional convex structures I: general results, Top. Appl. 14 (1982), 201–225.Google Scholar
23. van de Vel, M., Finite dimensional convex structures II: the invariants, Top. Appl. 16 (1983), 81–105.Google Scholar
24. van de Vel, M., On the rank of a topological convexity, Fund. Math. 119 (1984), 17–48.Google Scholar
25. van de Vel, M., Two dimensional convexities are join-hull commutative, Top. Appl. 16 (1983), 181–206.Google Scholar
26. van de Vel, M., Matching binary convexities, Top. Appl. 16 (1983), 207–235.Google Scholar
27. van de Vel, M., Binary convexities and distributive lattices, Proc. London Math. Soc. (3) 48 (1984), 1–33.Google Scholar
28. van de Vel, M., Dimension of binary convex structures, Proc. London Math. Soc. (3) 48 (1984), 34–54.Google Scholar
29. Verbeek, A., Superextensions of topological spaces, MC tract 41 (Amsterdam, 1972).Google Scholar